Page 11 - C110211

یهانتمان و یهانتم یاه هعومجم :لوا سرد

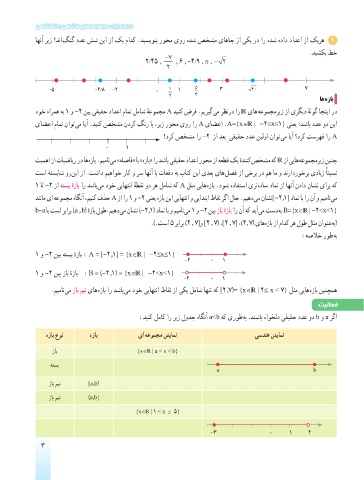
اهنآ ریز ؟دنا گنگ ددع شش نیا زا کی مادک .دیسیونب روحم یور هدش صخشم یاهاج زا یکی رد ار هدش هداد دادعا زا کیره 2

.دیشکب طخ
−7
2/45 , , 6 , -4/9 , π , − 2
2

-5 -2/8 -2 0 1 1 5 3 20 7
2 3
اه هزاب

دوخ هارمه هب 1 و -2 نیب یقیقح دادعا مامت لماش هعومجم A دینک ضرف .میریگ یم رظنرد ار R یاه هعومجمریز زا یرگید هنوگ اجنیا رد
ٔ
ٔ
یاضعا مامت ناوت یم ایآ .دینک صخشم ندرک گنر اب ،ریز روحم یور ار A یاضعا .A=}x∈R | -2≥x≥1{ ینعی ؛دشاب ددع ود نیا
؟درک صخشم ار -2 زا دعب یقیقح ددع نیلوا ناوت یم ایآ ؟درک تسرهف ار A

0 1 

تیمها زا تایضایر رد اه هزاب .میمان یم »هلصاف« ای »هزاب« ار دشاب یقیقح دادعا روحم زا هعطق کی هدننک صخشم هک R زا ییاه هعومجمریز نینچ
ٔ
تسا هتسیاش ور نیا زا .تشاد میهاوخ راک و رس اهنآ اب تاعفد هب باتک نیا یدعب یاه لصف زا یخرب رد مه ام و دنرادروخرب یدایز ًاتبسن
1 ات -2 زا هتسب هزاب ار دشاب یم دوخ ییاهتنا هطقن ود ره لماش هک A لثم ییاه هزاب .دوش هدافتسا یرت هداس دامن زا اهنآ نداد ناشن یارب هک
ٔ ٔ
دننام یا هعومجم هاگنآ ،مینک فذح A زا ار 1 و -2 ینعی هزاب نیا ییاهتنا و ییادتبا طاقن رگا لاح.میهد یم ناشن] -2,1[ دامن اب ار نآ و میمان یم

b-a اب تسا ربارب )a , b( هزاب لوط.میهد یم ناشن )-2 ,1( دامن اب و میمان یم 1 و -2 نیب زاب هزاب ار نآ هک دیآ یم تسد هب B=}x∈R | -2>x>1{
ٔ ٔ
.).تسا 5 ربارب )2 , 7[و ]2 , 7( ،]2 , 7[ ،)2, 7( یاه هزاب زا مادک ره لوط لاثم ناونع هب(
:هصلاخ روط هب

1 و -2 نیب هتسب هزاب : A = ]-2 ,1[ = }x∈R | -2≥x≥1{
ٔ -2 0 1

1 و -2 نیب زاب هزاب : B = )-2 ,1( = }x∈R | -2>x>1{
ٔ -2 0 1
.میمان یم زاب مین یاه هزاب ار دشاب یم دوخ ییاهتنا طاقن زا یکی لماش اهنت هک ]2 ,7(= }x∈R | 2≥ x > 7{ لثم ییاه هزاب نینچمه

تیلاعف
:دینک لماک ار ریز لودج هاگنآ a>b هک یروط هب ،دنشاب هاوخلد یقیقح ددع ود b و a رگا

هزاب عون هزاب یا هعومجم شیامن یسدنه شیامن

زاب }x∈R | a > x > b{

هتسب
a b

زاب مین ]a,b(
زاب مین )a,b[

}x∈R | 1 > x ≥ 5{

-3 0 1 2
3