Page 124 - C110211

عبات: 5 لصف

.دینک یسررب ار ریز یاه هرازگ یتسردان ای یتسرد 3

2
.تسا )0 +∞( زین نآ درب و )0 , +∞( ربارب f)x( =x -1 عبات هنماد )فلا
,
ُ ٔ
1
.تسا )2 +∞( نآ درب و یقیقح دادعا همه f (x) | x |= − عبات هنماد )ب
,
ُ ٔ 3 ٔ
.تسا )-∞ ,+∞( ربارب f)x( =2 تباث عبات هنماد )پ
ٔ
f( )
2
.f( ) =1 ،هاگنآ f)x( =2x+1 رگا )ت
2
مجح ،دشاب رتم 30 هناوتسا عافترا رگا .تسا هدش لیکشت ،هناوتسا یاهتنا ود رد r عاعش هب هرک مین ود و هناوتسا کی زا زاگ رکنات کی 4
.دیسیونب r زا یعبات بسح رب ار رکنات
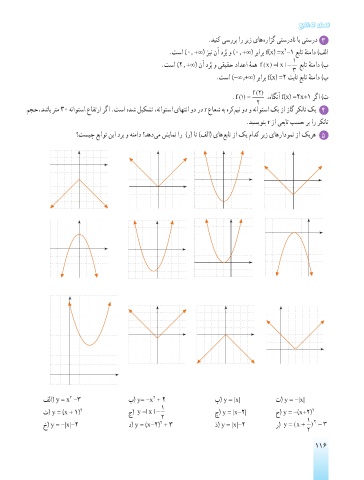
؟تسیچ عباوت نیا درب و هنماد ؟دهد یم شیامن ار )ر( ات )فلا( یاه عبات زا کی مادک ریز یاهرادومن زا کیره 5

2
2
فلا( y = x -3 ب( y= -x + 2 پ( y = |x| ت( y = -|x|
1
ث( y = )x + 1( 2 ج( y | x|= − چ( y = |x-2| ح( y = -)x+2( 2
2 1
2
خ( y = -|x|-2 د( y = )x-2( + 3 ذ( y = |x|-2 ر( y (x= + ) − 2 3
2
116