Page 46 - C110211

تاثلثم : 2 لصف

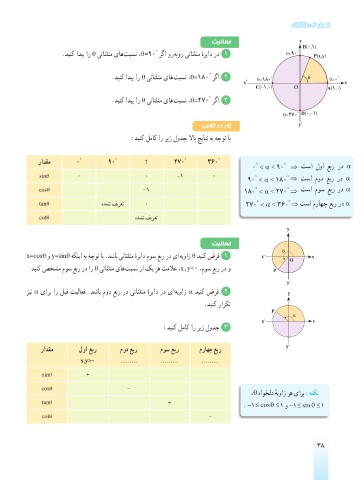
تیلاعف y
B)0,1(
°
.دينک اديپ ار θ یتاثلثم یاه تبسن ،θ=90 رگا ور هبور یتاثلثم هریاد رد 1 θ=90 °
ٔ P)x,y(
°
.دينک اديپ ار θ یتاثلثم یاه تبسن ،θ=180 رگا 2 ° θ °
x′ θ=180 θ=0 x
C)-1,0( O A)1,0(
°
.دينک اديپ ار θ یتاثلثم یاه تبسن ،θ=270 رگا 3
θ=270 ° D)0,-1(
سلاک رد راک y′

:دينک لماک ار ریز لودج لااب جیاتن هب هجوت اب

رادقم 0 ° 90 ° ؟ 270 ° 360 ° ° °
0 > α > 90 ⇒ تسا لوا عبر رد α
sinθ 0 0 -1 0 ° °
90 > α > 180 ⇒ تسا مود عبر رد α
°
cosθ -1 180 > α > 270 ° ⇒ تسا موس عبر رد α
°
tanθ هدشن فیرعت 0 270 > α > 360 ° ⇒ تسا مراهچ عبر رد α
cotθ هدشن فیرعت
y

تیلاعف
θ
x=cosθ و y=sinθ هکنیا هب هجوت اب .دشاب یتاثلثم هریاد موس عبر رد یا هیواز θ دينک ضرف 1 x′
ٔ O x
.دينک صخشم موس عبر رد ار θ یتاثلثم یاه تبسن زا کی ره تملاع ،x , y>0 ،موس عبر رد و P

y′
زين α یارب ار لبق تيلاعف .دشاب مود عبر رد یتاثلثم هریاد رد یا هیواز α دينک ضرف 2
ٔ y
.دينک رارکت
P
α
x′ x
:دينک لماک ار ریز لودج 3

y′
رادقم لوا عبر مود عبر موس عبر مراهچ عبر
x,y<0 ……… ……… ………

sinθ +

cosθ -
،θ هاوخلد هیواز ره یارب :هتکن
ٔ
tanθ +
. − ≤1 cosθ≤1 و − ≤1 sinθ≤1
cotθ -

38