Page 60 - C110211
P. 60
یربج یاه ترابع و ایوگ یاه ناوت : 3 لصف
.)دینک هدافتسا باسح نیشام زا دیناوت یم( دینک صخشم راشعا مقر کی اب ار ریز یلاکیدار دادعا زا مادک ره یبیرقت رادقم 2
5
5
3
/
10 7 25 16 64
رظانتم هک نییاپ روحم یور هدش صخشم طاقن زا یکی هب ار لااب روحم یور هدش صخشم طاقن زا کی ره ،ریز لکش رد هنومن دننام 3
.).دینک هئارا دروم ره زا یددع لاثم کی( دینک لصو ،تسا ددع نآ موس هشیر اب
ٔ
−2 a 4 −1 a 2 0 a 1 1 a 3
−2 b 4 a 4 c 4 −1 b 2 a 2 c 2 0 b 1 a 1 c 1 1 b 3 a 3 3 c
.دیهد خساپ ریز یاه لاؤس هب ،دیا هدرک کرد دادعا موس هشیر هرابرد هچنآ هب هجوت اب 4
ٔ
ٔ
3
a
؟دشاب دناوت یم یددع هچ a . a > و تسا تبثم یددع a )فلا
3
a
؟دشاب دناوت یم یدادعا هچ a . a = ینعی ؛تسا ربارب شدوخ اب نآ موس هشیر هک تسا یددع a )ب
ٔ
3
؟دشاب دناوت یم یدادعا هچ a . a < a و تسا تبثم یددع a )پ
.دیهد خساپ زین ،دشاب یفنم یددع a هک یتلاح یارب )پ( و )فلا( دراوم هب )ت
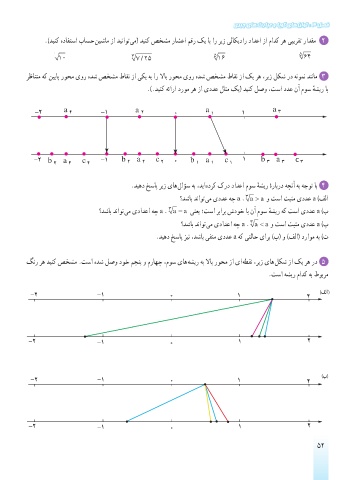
گنر ره دینک صخشم .تسا هدش لصو دوخ مجنپ و مراهچ ،موس یاه هشیر هب لااب روحم زا یا هطقن ،ریز یاه لکش زا کی ره رد 5
.تسا هشیر مادک هب طوبرم
−2 −1 0 1 2 )فلا(
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
)ب(
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2 52
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2
−2 −1 0 1 2