Page 69 - C110211

ایوگ یاه ناوت :موس سرد

سلاک رد راک
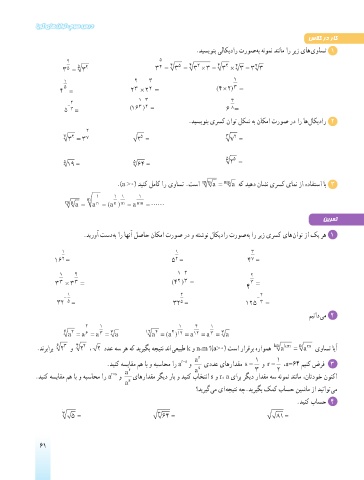
.دیسیونب یلاکیدار تروص هب هنومن دننام ار ریز یاه یواست 1

2 5
4
4
4
4
4
5
3
3 5 = 3 2 3 4 = 3 5 = 3 4 ×= 3 4 × 3 = 3 3
1 2 3 1
4 5 = 3 × 2 2 =2 ( × 42 ) = 3
4
13 3
4
− (16 34 8
) =
3
5 = 6 =
.دیسیونب یرسک ناوت لکش هب ناکما تروص رد ار اه لاکیدار 2
2
7 2 7 5 3 2
3 = 3 2 = 7 =

5 5
5
5 19= 64 = 2 =
.)a <0( دینک لماک ار یواست .تسا m n a = nm a هک دیهد ناشن یرسک یامن زا هدافتسا اب 3
1 11 1
m
m n a = a = (a ) = a mn =
n
n m
نیرمت
.دیروآ تسد هب ار اهنآ لصاح ناکما تروص رد و هتشون لاکیدار تروص هب ار ریز یرسک یاه ناوت زا کی ره 1

1 1 3
2
16 = 2 5 = 4 = 7
1 2 12 − 2
) =
3 × 3 3 = 3 (4 23 125 4 3 =
1 2 2
− −
5
5
32 = 32 = 125 3 =
میناد یم 2
2 1 1 4 1
6 a = a = a = 3 a a = (a ) = a 12 = a = 3 a
12 4
2
3
4 12
6
3
m
4 2
6 3
.دنربارب 2 و 2 ، 2 ددع هس ره هک دیریگب هجیتن دنا یعیبط k و n،m ؟)a<0( تسا رارقرب هراومه kn a km = n a یواست ایآ
a r 1 1
r-s
.دینک هسیاقم مه اب و هبساحم ار a و s یددع یاهرادقم s = و r = ،a=64 مینک ضرف 3
a r a 3 2
r-s
.دینک هسیاقم مه اب و هبساحم ار a و یاهرادقم رگید راب و دینک باختنا s و r، a یارب رگید رادقم هس هنومن دننام ،ناتدوخ نونکا
a s
؟دیریگ یم یا هجیتن هچ.دیریگب کمک باسح نیشام زا دیناوت یم
.دینک باسح 4
3 3
5 = 64 = 81=
61