Page 88 - C110211

اه هلداعمان و اه هلداعم : 4 لصف

2
ٔ
.دراد x = h هلداعم اب ینراقت طخ و )h , k( تاصتخم هب یسأر ، تسا a≠0 هک y = a)x-h( + k تروص هب یمهس ره

سلاک رد راک

.دینک مسر ار نآ سپس و صخشم ار سأر ،ریز یاه یمهس زا کی ره رد 1
2
2
y = -2 x +1 )ب y = )x+1( -2 )فلا

تیلاعف

2
.دیریگب رظن رد ار y =ax +bx+c تروص هب یمهس هلداعم
ٔ
:دیهد ناشن و دیسیونب لماک عبرم لکش هب ار هلداعم نیا تسار تمس فلا

b 4 ac b 2
−
2
y a(x + ) +
=
a 2 a 4
b 2
−
.تسا x =− زین نآ نراقت طخ و (− , ) ٔ هطقن ،یمهس نیا سأر هک دیهد ناشن ،لبق تمسق زا هدافتسا اب
1 b 4 ac b ب
a 2 a 2 a 4
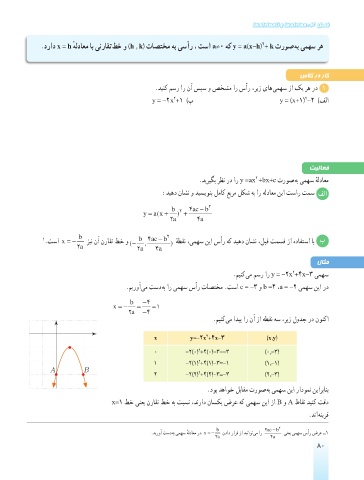
لاثم
.مینک یم مسر ار y = -2x +4x-3 یمهس
2
.میروآ یم تسد هب ار یمهس سأر تاصتخم .تسا c = -3 و b =4 ،a = -2 یمهس نیا رد

b −4
x =− = =1
a 2 −4
.مینک یم ادیپ ار نآ زا هطقن هس ،ریز لودج رد نونکا

2
x y=-2x +4x-3 )x,y(
2
0 -2)0( +4)0(-3=-3 )0,-3(
2
1 -2)1( +4)1(-3=-1 )1,-1(
A B
2
2 -2)2( +4)2(-3=-3 )2,-3(
.دوب دهاوخ لباقم تروص هب یمهس نیا رادومن نیاربانب
x=1 طخ ینعی نراقت طخ هب تبسن ،دنراد ناسکی ضرع هک یمهس نیا زا B و A طاقن دینک تقد

.دنا هنیرق

b 4 ac b 2
−
.دیروآ تسد هب یمهس ٔهلداعم رد x =− نداد رارق زا دیناوت یم ار ینعی یمهس سأر ضرع ــ1
a 2 a 4
80

NJ