Page 18 - C111215

هرازگ ود ِ یطرش ود بیکرت
p یطرش ود بیکرت ار نآ و میسیون یم »p ⇔q « تروص هب ار )p ⇒q( ∧ )q ⇒p( بکرم هرازگ ،دنشاب هرازگ ود q و p هاگره
ٔ
:میناوخ یم ریز تروص هب ار »p ⇔q « هرازگ .میمان یم q و
ٔ
»q رگا اهنت و رگا p« و »تسا q یارب یفاک و مزلا طرش p« ،»سکعرب و q هاگ نآ ،p رگا«
.تساه هرازگ یطرش ود بیکرت زا یا هنومن ،ریز یاه هرازگ :لاثم
2 > 5 ⇔ تسا لوا ددع 6 )فلا
ّ
.تسایوگ یددع 2 ⇔ تسین لوا ددع 99 )ب
ّ
.دشاب یهت دماشیپ هک تسا نآ ،دشاب رفص اب ربارب یدماشیپ لامتحا هکنآ یارب یفاک و مزلا طرش ،سات کی باترپ رد )پ
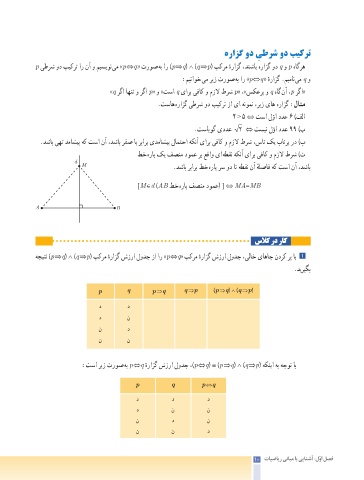
طخ هراپ کی فصنم دومع رب عقاو یا هطقن هکنآ یارب یفاک و مزلا طرش )ت
d
M .دشاب ربارب طخ هراپ رس ود ات هطقن نآ هلصاف هک تسا نآ ،دشاب
ٔ

]M∈d )AB طخ هراپ فصنم دومع( [ ⇔ MA=MB

A B

سلاک رد راک
رد
سلا
ک
ک
را

هجیتن )p ⇒ q( ∧ )q ⇒p( بکرم هرازگ شزرا لودج زا ار »p ⇔q« بکرم هرازگ شزرا لودج ،یلاخ یاهاج ندرک رپ اب 1
ٔ ٔ
.دیریگب
p q p ⇒q q ⇒p )p ⇒q( ∧ )q ⇒p(

د د

د ن
ن د
ن ن

:تسا ریز تروص هب p ⇔q هرازگ شزرا لودج ،)p ⇔q( ≡ )p ⇒q( ∧ )q ⇒p( هکنیا هب هجوت اب
ٔ

p q p ⇔q

د د د
د ن ن
ن د ن
ن ن د

10 تایضایر ینابم اب ییانشآ :لّ وا لصف