Page 29 - C111215

اه هعومجم نیب لامعا و نیناوق

عمج لمع ود یارب و یقیقح دادعا رد امش ،میزادرپ یم کارتشا و عامتجا لامعا هب طوبرم صاوخ و نیناوق یسررب هب لاح
ِ
:میناد یم ینعی ؛دیسانش یم ار عمج هب تبسن برض یریذپ عیزوت و یریذپ تکرش ،ییاج هباج نوچ ینیناوق )*( برض و )+(
I(∀ a,b∈  ؛ a+b=b+a ییاج هباج تیصاخ
+
=
+
+
a + (bc )(a b ) c
II(∀ a,b,c∈  ؛  یریذپ تکرش تیصاخ
bc =
a
b
 a ×( × ) ( × )×c
III(∀ a,b,c∈ ؛ a *(b+c)=(a *b(+)a *c( » + « هب تبسن » * « یریذپ عیزوت تیصاخ
.)دیهد ناشن ار بلطم نیا ضقن لاثم کی رکذ اب( ،تسین ریذپ عیزوت * لمع هب تبسن + لمع هک دیراد هجوت
یارب اه هرازگ رد هک یصاوخ هب هجوت اب صاوخ نیا و هتشاد قوف صاوخ هباشم یصاوخ  و  لمع ود اه هعومجم رد
ار صاوخ نیا یرارقرب نو رادومن طسوت ادتبا ،ریز تیلاعف رد .دنشاب یم تابثا و یسررب لباق دش نایب » ˄ « و » ˅ « بیکرت ود

.دینک یم هدهاشم

تیلاعف
تیلاعف
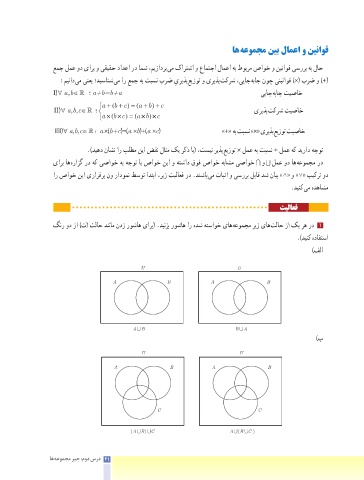
گنر ود زا )ت( تلاح دننام ندز روشاه یارب( .دینزب روشاه ار هدش هتساوخ یاه هعومجم ریز یاه تلاح زا کی ره رد 1

.)دینک هدافتسا
)فلا

U U

A B A B

A  B B  A
)ب

U U

A B A B

C C

(A B) C A (B C )

اه هعومجم ربج :مود سرد 21