Page 39 - C111215

تیلاعف
تیلاعف
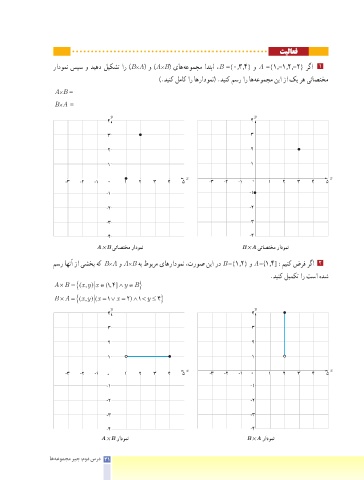
رادومن سپس و دیهد لیکشت ار )B×A( و )A×B( یاه هعومجم ادتبا ،B =}0,3,4{ و A =}1,-1,2,-2{ رگا 1
).دینک لماک ار اهرادومن( .دینک مسر ار اه هعومجم نیا زا کی ره یتاصتخم

A×B =
B×A =

y y
4 4
3 3

2 2

1 1

x x
-3 -2 -1 0 1 2 3 4 5 -3 -2 -1 0 1 2 3 4 5
-1 -1

-2 -2

-3 -3
-4 -4

A×B یتاصتخم رادومن B×A یتاصتخم رادومن

مسر اهنآ زا یشخب هک B×A و A×B هب طوبرم یاهرادومن ،تروص نیا رد B =}1,2{ و A = )1,4] :مینک ضرف رگا 2
.دینک لیمکت ار تسا هدش
y
14
A ×B = {( , ) ∈xy x (, ]∧∈B }
B A = {( , )(xy x = ∨ =1 x 2 ) ∧ < ≤ } 4
×
y
1
y y
4 4
3 3

2 2
1 1

x x
-3 -2 -1 0 1 2 3 4 5 -3 -2 -1 0 1 2 3 4 5
-1 -1

-2 -2

-3 -3

-4 -4
A×B رادومن B×A رادومن

اه هعومجم ربج :مود سرد 31