Page 39 - C111213
P. 39
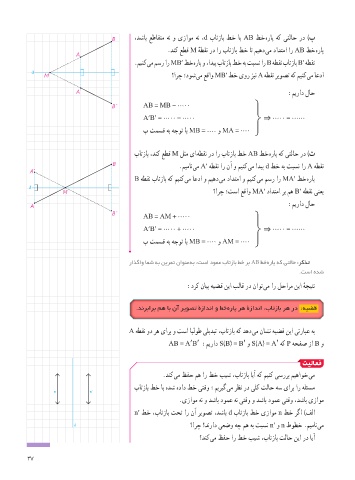
B ،دشاب عطاقتم هن و یزاوم هن ،d باتزاب طخ اب AB طخ هراپ هک یتلاح رد )پ
.دنک عطق M هطقن رد ار باتزاب طخ ات میهد یم دادتما ار AB طخ هراپ
A ٔ
.مینک یم مسر ار MB′ طخ هراپ و ،ادیپ باتزاب طخ هب تبسن ار B هطقن باتزاب B′ هطقن
d
M ؟ارچ ؛دوش یم عقاو MB′ طخ یور زین A هطقن ریوصت هک مینک یم اعدا
A´ :میراد لاح
B´ AB = MB - …..
-
A′B′ = ….. ….. ⇒ ….. ……
=
ب تمسق هب هجوت اب MB = …. و MA = ….
باتزاب ،دنک عطق M لثم یا هطقن رد ار باتزاب طخ AB طخ هراپ هک یتلاح رد )ت
B .میمان یم A′ هطقن ار نآ و مینک یم ادیپ d طخ هب تبسن ار A هطقن
A´
B هطقن باتزاب هک مینک یم اعدا و میهد یم دادتما و مینک یم مسر ار MA′ طخ هراپ
d
M ؟ارچ ؛تسا عقاو MA′ دادتما رب مه B′ هطقن ینعی
A :میراد لاح
B´ AB = AM + …..
+
A′B′ = ….. ….. ⇒ ….. ……
=
ب تمسق هب هجوت اب MB = …. و AM = ….
راذگاو امش هب نیرمت ناونع هب ،تسا دومع باتزاب طخ رب AB طخ هراپ هک یتلاح :رکذت
.تسا هدش
:درک نایب هیضق نیا بلاق رد ناوت یم ار لحارم نیا هجیتن
ٔ
.دنربارب مه اب نآ ریوصت ۀزادنا و طخ هراپ ره ۀزادنا ،باتزاب ره رد :هیضق
A هطقن ود ره یارب و تسا اپلوط یلیدبت ،باتزاب هک دهد یم ناشن هیضق نیا یترابع هب
AB = A′B′ :میراد S)B( = B′ و S)A( = A′ هک P هحفص زا B و
.دنک یم ظفح مه ار طخ بیش ،باتزاب ایآ هک مینک یسررب میهاوخ یم
باتزاب طخ اب هدش هداد طخ یتقو :میریگ یم رظن رد یلک تلاح هس یارب ار هلئسم
n n´
.یزاوم هن و دشاب دومع هن یتقو و دشاب دومع یتقو ،دشاب یزاوم
n′ طخ ،باتزاب تحت ار نآ ریوصت ،دشاب d باتزاب طخ یزاوم n طخ رگا )فلا
d ؟ارچ ؟دنراد یعضو هچ مه هب تبسن n′ و n طوطخ .میمان یم
؟دنک یم ظفح ار طخ بیش ،باتزاب تلاح نیا رد ایآ
37