Page 54 - C111213
P. 54
.داد ماجنا ناوت یم هنوگچ ار لمع نیا هک دیهد حیضوت ریوصت نیا کمک هب B
C´
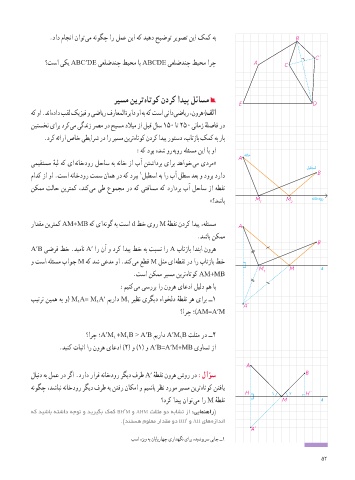
؟تسا یکی ABC′DE یعلضدنچ طیحم اب ABCDE یعلضدنچ طیحم ارچ A C
ریسم نیرت هاتوک ندرک ادیپ لئاسم
E D
هک وا .دنا هداد بقل کیزیف و یضایر فراعملاةریاد وا هب هک تسا یناد یضایر ،نوره )فلا
نیتسخن یارب درک یم یگدنز رصم رد حیسم دلایم زا لبق لاس 150 ات 250 ینامز هلصاف رد
ٔ
.درک هئارا صاخ یطیارش رد ار ریسم نیرت هاتوک ندرک ادیپ روتسد ،باتزاب کمک هب راب
:هک دوب هدش ور هبور هلئسم نیا اب وا
A هناخ
یمیقتسم هبل هک یا هناخدور لحاس هب هناخ زا بآ نتشادرب یارب دهاوخ یم یدرم« لبطسا
ٔ
1
مادک زا وا .تسا هناخدور تمس نامه رد هک دربب لبطسا هب ار بآ لطس دعب و دورب دراد B
نکمم تلاح نیرتمک ،دنک یم یط عومجم رد هک یتفاسم هک درادرب بآ لحاس زا هطقن
»؟دشاب M 1 M 2 هناخدور
رادقم نیرتمک AM+MB هک یا هنوگ هب تسا d طخ یور M هطقن ندرک ادیپ ،هلئسم A
ٔ
.دشاب نکمم
B
A′B یضرف طخ .دیمان A′ ار نآ و درک ادیپ طخ هب تبسن ار A باتزاب ادتبا نوره
و تسا هلئسم باوج M هک دش یعدم وا .دنک یم عطق M لثم یا هطقن رد ار باتزاب طخ
M M d
.تسا نکمم ریسم نیرت هاتوک AM+MB 1
:مینک یم یسررب ار نوره یاعدا لیلد مه اب
بیترت نیمه هب و( M A= M A′ میراد M ریظن یرگید هاوخلد هطقن ره یارب ــ1
ٔ
1
1
1
A´
؟ارچ ؛)AM=A′M
؟ارچ ؛A′M +M B < A′B میراد A′M B ثلثم رد ــ2
1
1
1
.دینک تابثا ار نوره یاعدا )2( و )1( و A′B=A′M+MB یواست زا
A
لابند هب لمع رد رگا .دراد رارق هناخدور رگید فرط A′ هطقن نوره شور رد :لاؤس B
ٔ
هنوگچ ،دشابن هناخدور رگید فرط هب نتفر ناکما و میشاب رظن دروم ریسم نیرت هاتوک نتفای
H 1 2 H´
؟درک ادیپ ناوت یم ار M هطقن M d
ٔ
هک دیشاب هتشاد هجوت و دیریگب کمک BH′M و AHM ثلثم ود هباشت زا :ییامنهار(
.)دنتسه مولعم رادقم ود BH′ و AH یاه هزادنا
A´
بسا هژیو هب نایاپراهچ یرادهگن یارب هدیشوپرس ییاج ــ1
52