Page 114 - C111214

106

دامن زا ای تسا هجرد بسح رب x دوش هتفگ ًاحیرص هکنآ رگم دنریگ یم رظن رد نایدار بسحرب ار x هشیمه ،y = sin x عبات رد 4
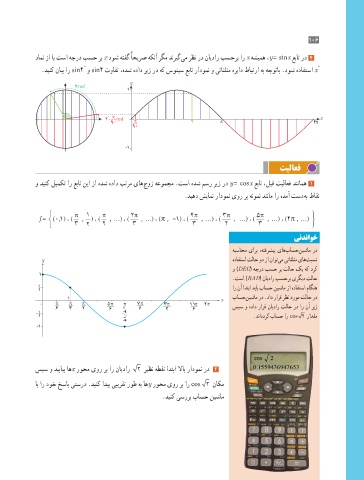
.دینک نایب ار sin2 و sin2 توافت ،هدش هداد ریز رد هک سونیس عبات رادومن و یتاثلثم هریاد طابترا هب هجوتاب .دوش هدافتسا x °
°
y
2 rad
1

2 0 = π rad π x
90 2 π π 2
90

-1

تیلاعف

و دینک لیمکت ار عبات نیا زا هدش هداد بترم یاه جوز هعومجم .تسا هدش مسر ریز رد y = cos x عبات ،لبق تیلاعف دننامه 1
.دیهد شیامن رادومن یور رب هنومن دننام ار هدمآ تسد هب طاقن

 π 1 π 2 π 4 π 3 π 5 π 
f =  (0,1) ، ( , ) ، ( , …) ، ( , …) ، (π , -1) ، ( , …) ، ( , …) ، ( , …) ، (2π , …) 
 3 2 2 3 3 2 3 

یندناوخ
یندناوخ
هبساحم یارب ،هتفرشیپ یاه باسح نیشام رد
y هدافتسا تلاح ود زا ناوت یم یتاثلثم یاه تبسن
و )DEG( هجرد بسح رب تلاح کی هک درک
1
.تسا )RAD ( نایدار بسحرب یرگید تلاح
1
2 ار نآ ادتبا دیاب باسح نیشام زا هدافتسا ماگنه
1 x باسح نیشام رد .داد رارق رظن دروم تلاح رد
0 π π π 5 π 7 π 3 π 11 π 2 π
6 3 2 6 π  6 2 6 سپس و هداد رارق نایدار تلاح رد ار نآ ریز
− 1 3/
2 14 .دنا هدرک باسح ار cos 2 رادقم
-1

سپس و دیبایب اهx روحم یور رب ار نایدار 2 ریظن هطقن ادتبا لااب رادومن رد 2

اب ار دوخ خساپ یتسرد .دینک ادیپ یبیرقت روط هب اهy روحم یور رب ار cos 2 ناکم
.دینک یسررب باسح نیشام