Page 117 - C111214

109 تاثلثم : مراهچ لصف

نیرمت

.دینک ریظن هدش هداد یاهرادومن اب ار ریز یتاثلثم عباوت 1

π π
y = sin)x − ( )پ y = cos)x + ( )ب y = - |sin x | )فلا
3 6
y y y

1 1 1
x x x
0 π π 2 −π 0 π 0 π π 2
-1 -1 -1

هدش هداد یتاثلثم عباوت ،هدش مسر شخب هب هجوت اب .تسا هدش مسر یتاثلثم عبات کی زا یشخب ریز یاهرادومن زا کی ره رد 2
.دیزاس لماک ار رادومن سپس و دینک ریظن اهرادومن هب ار ریز رد

π π
y =1+ |cos x | )پ y = cos)x − ( -1 )ب y =− sin)x + ( )فلا
3 6

y y y

1 1 1
x x x
−π − π 0 π π 2 −π 0 π π π 3 2 π −π 0 π π 2 π
6 2 2 3
-1 -1 -1

53cm عباوت رادقم نیرتمک و نیرتشیب ،2 لاؤس رد لااب یاهرادومن هب هجوت اب 3
153cm ؟دهد یم خر یطاقن هچ رد لاؤس نآ رد هدش هداد یتاثلثم
100cm α
نآ رد هدش هداد یتاثلثم عباوت زا کی مادک ،2 لاؤس یاهرادومن هب هجوت اب 4
θ θ ؟تسا کی هب کی )0, π( هزاب رد لاؤس
ٔ
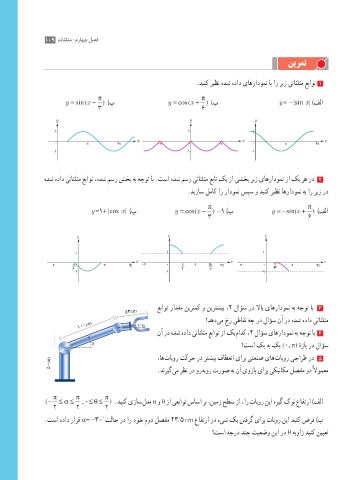
50cm 50cm ،اه تابور تکرح رد رتشیب فاطعنا یارب یتعنص یاه تابور یحارط رد 5
.دنریگ یم رظن رد ور هبور تروص هب نآ یوزاب یارب یکیناکم لصفم ود لاومعم
ً

π π π
)− ≤α ≤ , ≤θ ≤ ( .دینک یزاس لدم α و θ زا یعباوت ساسا رب ،نیمز حطس زا ،ار تابور نیا هریگ کون عافترا )فلا
0
2 2 2
.تسا هداد رارق α= -30 تلاح رد ار دوخ مود لصفم 23/5 cm عافترا رد ءیش کی نتفرگ یارب تابور نیا دینک ضرف )ب
°
؟تسا هجرد دنچ تیعضو نیا رد θ هیواز دینک نییعت