Page 12 - C111214

4

سلاکردراک

n
)a +
n ( S = 1 a :هاگنآ دنشاب رخآ و لوا تلامج بیترت هب a n و a رگا یباسح هلابند کی رد دیهد ناشن 1
n
1
2
.دیروآ تسد هب ار 4 برضم یمقر ود یعیبط یاهددع ٔهمه عومجم 2

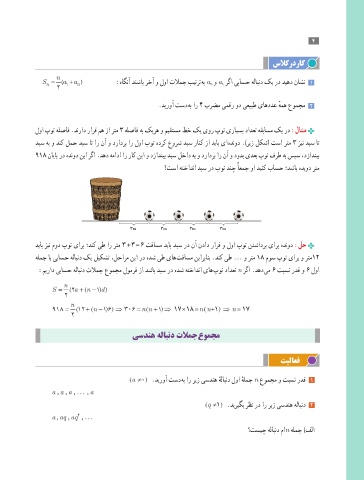
لوا پوت هلصاف .دنراد رارق مه زا رتم 3 هلصاف هب کیره و میقتسم طخ کی یور پوت یرایسب دادعت هقباسم کی رد :لاثم

دبس هب و دنک لمح دبس ات ار نآ و درادرب ار لوا پوت هدرک عورش دبس رانک زا دیاب یا هدنود .)ریز لکش( تسا رتم 3 زین دبس ات
918 نایاپ رد هدنود نیا رگا .دهد همادا ار راک نیا و دزادنیب دبس لخاد هب و درادرب ار نآ و دودب یدعب پوت فرط هب سپس ،دزادنیب

؟تسا هتخادنا دبس رد پوت دنچ ًاعمج وا دینک باسح ؛دشاب هدیود رتم

3 m 3 m 3 m 3 m

دیاب زین مود پوت یارب ؛دنک یط ار رتم 3 + 3 = 6 تفاسم دیاب دبس رد نآ نداد رارق و لوا پوت نتشادرب یارب هدنود :لح
هلمج اب یباسح هلابند کی لیکشت ،لحارم نیا رد هدش یط یاه تفاسم نیاربانب .دنک یط ... و رتم 18 موس پوت یارب و رتم12

:میراد یباسح هلابند تلامج عومجم لومرف زا دشاب دبس رد هدش هتخادنا یاه پوت دادعت n رگا .دهد یم 6 تبسن ردق و 6 لوا

n
S = ) a +2 )n − 1 ((
d
2
n
= 918 )12 + )n − (( ⇒ 16 = 306 ) nn + ( 1 ⇒ 17 * 18 = n ( n +1( ⇒ n = 17
2

یسدنه هلابند تلامج عومجم

تیلاعف

ٔ
ٔ
)a ≠0( .دیروآ تسد هب ار ریز یسدنه هلابند لوا هلمج n عومجم و تبسن ردق 1
a , a , a , ... , a
)q ≠1( .دیریگب رظن رد ار ریز یسدنه هلابند 2
2
a, aq , a q , ...

؟تسیچ هلابند ماn هلمج )فلا