Page 125 - C111214

117 یگتسویپ و دح : مجنپ لصف

سلاکردراک

2
x + x ≠ 3 x −9
3
hx
:دیریگب رظنرد ار () =  و ()gx = ، f (x) = x +3 یاه هطباض اب h و g ، f عباوت

4
3
 x = x − 3
:دیروآ تسد هب دنشاب هدش فیرعت هک یتروص رد ار ریز ریداقم 1
f (3) = .... g (3) = .... h (3) = ....

یددع هچ هب مادکره h و g ، f عباوت ریداقم ،مینک یم کیدزن 3 ددع هب ار x ریداقم یتقو هک دینزب سدح ،ریز لودج لیمکت اب 2
.دنوش یم کیدزن

x 2/9 2/99 2/999 2/9999 → 3 ← 3/0000١ 3/000١ 3/00١ 3/0١ 3/١

f (x( 5/9 5/99 5/999 5/9999 → ? ← 6/0000١ 6/000١ 6/00١ 6/0١ 6/١

g x( .... .... .... .... → ? ← .... .... .... .... ....
(
h x( .... .... .... .... → ? ← .... .... .... .... ....
(

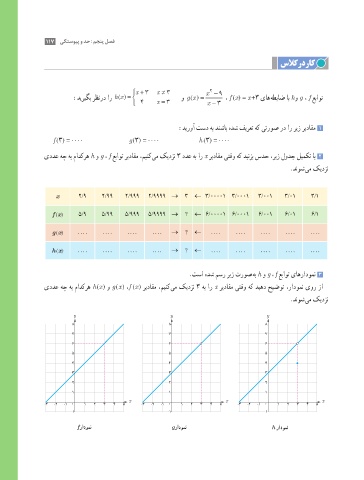
.تسا هدش مسر ریز تروص هب h و g ، f عباوت یاهرادومن 3
یددع هچ هب مادکره h (x ) و g ( x ) ،f (x ) ریداقم ،مینک یم کیدزن 3 هب ار x ریداقم یتقو هک دیهد حیضوت ،رادومن یور زا

.دنوش یم کیدزن

y y y
8 8 8
7 7 7
6 6 6
5 5 5
4 4 4
3 3 3
2 2 2
1 1 1
x x x
-3 -2 -1 0 1 2 3 4 5 -3 -2 -1 0 1 2 3 4 5 -3 -2 -1 0 1 2 3 4 5
-1 -1 -1

fرادومن gرادومن h رادومن