Page 128 - C111214

120

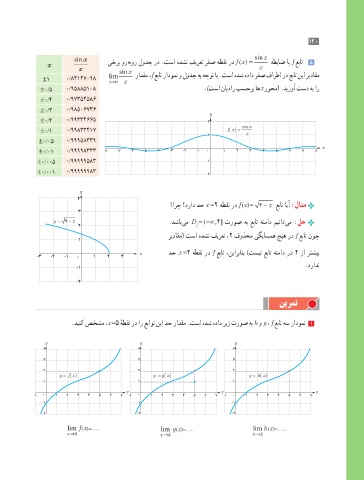
sinx یخرب ور هبور لودج رد .تسا هدشن فیرعت رفص هطقن رد ()f x = sinx
x هطباض اب f عبات 5
x sinx x

±1 0/84١47098 lim رادقم ،f عبات رادومن و لودج هب هجوت اب .تسا هدش هداد رفص فارطا رد عبات نیا ریداقم
x →0 x
±0/5 0/95885١08 .)تسا نایدار بسحرب اهx روحم( .دیروآ تسد هب ار
±0/4 0/97354586
±0/3 0/98506736
y
±0/2 0/99334665 2
sin x
±0/1 0/998334١7 f(x) =
1 x
±0/05 0/99958339
x
±0/01 0/99998333 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
±0/005 0/99999583 -1
±0/001 0/99999983 -2

y
4
؟ارچ ؟دراد دح x =2 هطقن رد f (x) = 2 −x عبات ایآ :لاثم

3
y = 2 − x .دشاب یم D = (-∞ , 2] تروص هب عبات هنماد میناد یم :لح
2 f
ریداقم( تسا هدشن فیرعت ،2 فوذحم یگیاسمه چیه رد f عبات نوچ
1

x دح x =2 هطقن رد f عبات ،نیاربانب )تسین عبات هنماد رد 2 زا رتشیب
-3 -2 -1 0 1 2 3
.درادن
-1

-2

نیرمت

ٔ
.دینک صخشم ،x =5 هطقن رد ار عباوت نیا دح رادقم .تسا هدش هداد ریز تروص هب h و g ، f عبات هس رادومن 1

y y y
4 4 4
3 3 3
2 2 2
y = f(x) y = g(x) y = h(x)
1 1 1
x x x
-1 0 1 2 3 4 5 6 7 -1 0 1 2 3 4 5 6 7 -1 0 1 2 3 4 5 6 7
-1 -1 -1
-2 -2 -2

(
lim f (x)=.... lim g x)=.... lim h (x)=....
x→5 x→5 x→5