Page 139 - C111214

131 یگتسویپ و دح : مجنپ لصف

تیلاعف

2
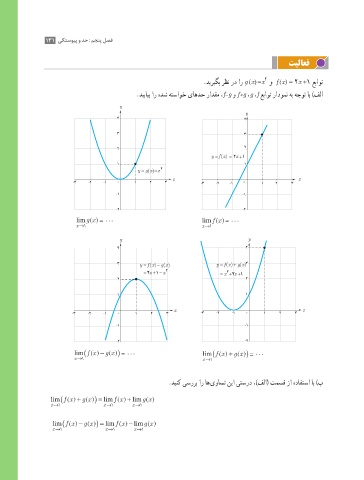
.دیریگب رظن رد ار g (x) =x و f (x( = 2x +1 عباوت

.دیبایب ار هدش هتساوخ یاهدح رادقم ،f-g و f +g ،g ،f عباوت رادومن هب هجوت اب )فلا

y
y
4 4

3 3

2 2
f(x) x
y = = +
2 1
1 1
y = g(x) x 2
=
x x
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
-1 -1

-2 -2
gx
f
x
lim ( ( = ... lim ( (= ...
x→1 x→1
y y y y
4 4 4 4

3 3 y = f( y −x) g(x) − y = f( y +x) g(x) + 3 3
= f(x) g(x)
= f(x) g(x)
2
= x2 x−
2
1
= x2 +1 + − x 2 = x +2 x +2 x +1
2
= x +1
2 2 2 2
1 1 1 1
x x x x
-3 -3 -2 -2 -1 -10 0 1 1 2 2 3 3 -3 -3 -2 -2 -1 -10 0 1 1 2 2 3 3
-1 -1 -1 -1
-2 -2 -2 -2
((
lim ( ((f x − gx ) = ... lim ( ((f x + gx )= ...
((
x→1 x→1

.دینک یسررب ار اه یواست نیا یتسرد ،)فلا( تمسق زا هدافتسا اب )ب

lim ( (( +f x gx ) lim (( lim ((= f x + gx
((
x lim ( (( +f x gx ) lim (( lim ((= x →1 f x + x →1 gx
→1
((
( (( −gx
lim f x (( ) lim (( lim ((= x →1 f x − x →1 gx
x
→1
x →1 x →1 x →1
−
(( =
lim ( (( −f x gx ) lim (( lim ((
f x
gx
x →1 x →1 x →1