Page 141 - C111214

133 یگتسویپ و دح : مجنپ لصف

رد یگمه f n ،...، f عباوت و یعیبط ددع کی n رگا ،ینعی .درک نایب زین رتشیب و عبات هس یارب ناوت یم ار لبق هیضق :رکذت
1
:هاگ نآ ،دنشاب هتشاد دح x =a هطقن

lim ( ()fx + 1 + f n () ) = lim () +  + lim f n ()
x
x
fx
1
x→ a x→ a x→ a
lim ( ()fx × 1 × f n () ) = lim ()×  × lim f n ()
x
x
fx
1
x→ a x→ a x→ a
)
n
n
lim ( ( )f x ) = ( lim ( ) :هاگ نآ دشاب هتشاد دح x =a هطقن رد f عبات رگا ،هژیو هب
f
x
x →a x →a
n
lim x n = a :دوش یم هجیتن ،مینک باختنا f (x) =x ینامه عبات ار f عبات رگا ،صاخ تلاح رد هک
x→ a
3 x <1  x 2 x < 2
 −1
f
x
.دیریگب رظن رد ار ()gx =  و () =  عبات ود :لاثم
 4 − x x ≥1   x −5 x ≥ 2
f
.دیروآ تسد هب x =2 هطقن رد ار و f.g ،f - g ،f + g عباوت دح
g
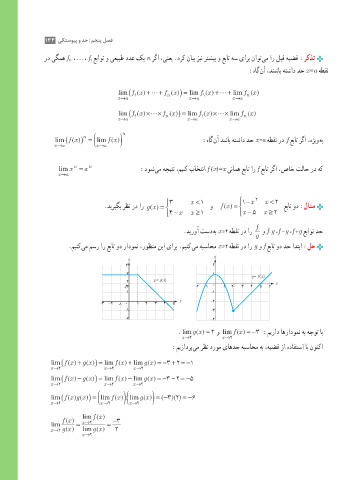
.مینک یم مسر ار عبات ود رادومن ،روظنم نیا یارب .مینک یم هبساحم x =2 هطقن رد ار g و f عبات ود دح ادتبا :لح
y
y
4 2
3 1 y= f(x)
2 y = g(x) x
3 -2 -1 0 1 2 3 4 5 6
1 -1
-3 -2 -1 0 1 2 3 4 5 x -2
-1 -3
-2 -4
gx
x
f
. lim ( ) = 2 و lim ( ) =−3 :میراد اهرادومن هب هجوت اب
x→2 x→2
:میزادرپ یم رظن دروم یاهدح هبساحم هب ،هیضق زا هدافتسا اب نونکا
lim ( ()f x + gx ) = lim () lim () =− + =−1
()
+
32
gx
x
f
x→2 x→2 x→2
()
lim ( ()f x − gx ) = lim () lim () =− − =−5
−
f
x
32
gx
x→2 x→2 x→2
)
)(
lim ( () ()f x gx ) = ( lim () lim () = (−3 )( ) =−6
2
gx
x
f
x→2 x→2 x→2
lim ( )
x
f
f () x −3
lim = x→2 =
()
gx
x→2 gx lim () 2
x→2