Page 148 - C111214

140

.دیریگب رظن رد ار ریز عباوت 5

 −2 x <1
2
y =3x +2 , y =x -1 , y =[x]-1 y = 
 2 x >1
.دیبایب )دوجو تروص رد( ار x =1 رد قوف عباوت زا کی ره دح رادقم )فلا

.دینک لماک ار ریز لودج ،قوف عبات راهچ نیب زا g و f عباوت باختنا اب )ب

f (x)+g (x) =… g (x) = … f (x) = … .دنراد دح 1 رد f +g و g ، f عبات هس ره

f (x) g (x) = … g (x) = … f (x) = … .درادن دح 1 رد f عبات اما دراد دح 1 رد f.g عبات

f () x = … … … f
()
gx g (x) = f (x) = .درادن تسار دح 1 رد عبات اما دنراد تسار دح1 رد g و f عباوت
g
2
2
f (x) = … f (x) = … .درادن دح 1 رد f عبات اما دراد دح 1 رد f عبات
x
f () = … f (x)= … .درادن دح 1 رد f عبات اما دراد دح 1 رد f عبات

؟تفگ ناوت یم هچ a رد f +g عبات دح دوجو دروم رد دشاب هتشادن دح a رد g عبات اما دشاب دوجوم a رد f عبات دح رگا 6

:دشاب هتشاد دح x = -1 رد ریز عبات هک دینک نییعت یروط ار b رادقم 7

 x + [] x
2

x
x
f () =  || x <−1

+
 3 xb x >−1
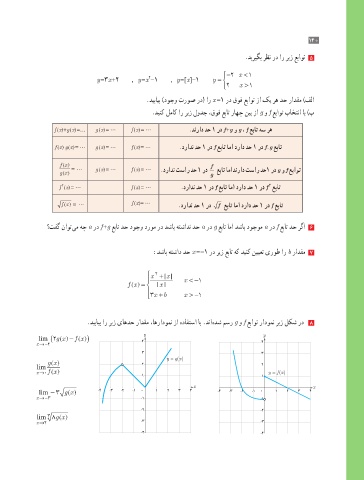
.دیبایب ار ریز یاهدح رادقم ،اهرادومن زا هدافتسا اب .دنا هدش مسر g و f عباوت رادومن ریز لکش رد 8
−
lim ( gx2 () f () ) y y
x
x→−2 4 4
3 3
y = gx
()
()
lim gx 2 2
x→0 f () x y = fx
()
1 1
x x
( )
lim − 3 gx -4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4
x→−3 -1 -1
-2 -2
( )
3
lim 8 gx
x→2 -3 -3
-4 -4