Page 18 - C111214

10

عبات یاهرفص

تیلاعف

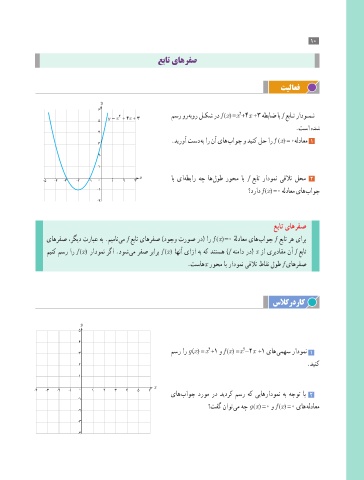
y
6 2

y = x + 2 x + 4 3 مسر ور هبور لـکش رد f (x) = x +4x +3 هطباض اب f عباـت رادوـمـن
5
.تسا هدش
4
.دیروآ تسد هب ار نآ یاه باوج و دینک لح ار f (x) = 0هلداعم 1
3
2

1
x اب یا هطبار هچ اه لوط روحم اب f عبات رادومن یقلات لحم 2
-5 -4 -3 -2 -1 0 1 2 3
-1 ؟دراد f (x) =0 هلداعم یاه باوج

-2

عبات یاهرفص

یاهرفص ،رگید ترابع هب .میمان یم f عبات یاهرفص (دوجو تروص رد) ار f (x) =0 هلداعم یاه باوج f عبات ره یارب
ٔ
مینک مسر ار f (x) رادومن رگا .دوش یم رفص ربارب f (x) اهنآ یازا هب هک دنتسه (f هنماد رد) x زا یریداقم نآ f عبات

.تساهx روحم اب رادومن یقلات طاقن لوط f یاهرفص

سلاکردراک

y
5

4
2 2
3 مسر ار g (x) = x +1 و f (x) = x -2x +1 یاه یمهس رادومن 1
2 .دینک
1
x
-4 -3 -2 -1 0 1 2 3 4 5 6
یاه باوج دروم رد دیدرک مسر هک ییاهرادومن هب هجوت اب 2
-1
؟تفگ ناوت یم هچ g (x) =0 و f (x) =0 یاه هلداعم
-2

-3
-4