Page 19 - C111214

11 هلداعم و ربج : لوا لصف

2
دیهد ناشن دنشاب f (x) = ax + bx +c مود هجرد عبات یاهرفص x ʺ و x ʹ رگا :لاثم
ax + bx + c = a(x -x ʹ) (x -x ʺ)
2
2
2
و دنتسه ax + bx +c =0 هلداعم یاه باوج سپ دنتسه f (x) = ax + bx +c عبات یاهرفص x ʺ و x ʹ هک اجنآ زا :لح
:میراد
ʹ
a (x -x ʹ)(x -x ʺ) = a (x -(x +x ʺ)x +x x ʺ)
ʹ
2
= a (x -Sx +p)
2
2
= [ ax − ( b − )x + c ]
a a
2
= a x + b x +c
2
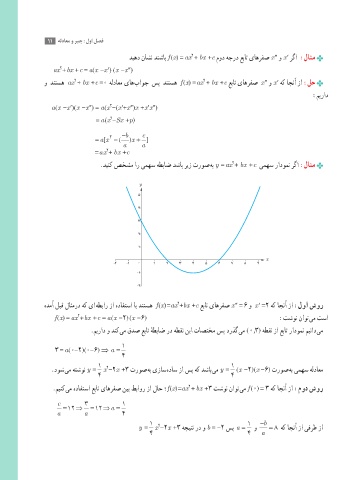
.دینک صخشم ار یمهس هطباض دشاب ریز تروص هب y = ax + bx + c یمهس رادومن رگا :لاثم

y
5

4

3
2

1
x
-2 -1 0 1 2 3 4 5 6 7 8 9
-1
-2

2
هدمآ لبق لاثمرد هک یا هطبار زا هدافتسا اب دنتسه f (x) =ax +bx +c عبات یاهرفص x ʺ = 6 و x ʹ =2 هک اجنآ زا :لوا شور
2
f (x) = ax + bx + c = a (x -2) (x -6) :تشون ناوت یم تسا
.میراد و دنک یم قدص عبات هطباض رد هطقن نیا تاصتخم سپ درذگ یم ( 0,3) هطقن زا عبات رادومن میناد یم
ٔ
1
3 = a (0-2)(0-6) ⇒ a =
4
1 1
2
.دوش یم هتشون y = x -2x +3 تروص هب یزاس هداس زا سپ هک دشاب یم y = (x -2)(x -6) تروص هب یمهس هلداعم
4 4
2
.مینک یم هدافتسا عبات یاهرفص نیب طباور زا لاح ؛ f (x) =ax + bx +3 تشون ناوت یم f (0) = 3 هک اجنآ زا :مود شور

c =12 ⇒ 3 =12 ⇒ a = 1
a a 4
1 1 b −
2
y = x -2x +3 هجیتن رد و b = -2 سپ a = و = 8 هک اجنآ زا یفرط زا
4 4 a