Page 20 - C111214

y
y y x
x
y y
y
x
12
y x
x y
y x
سلاکردراک
y
y
x x
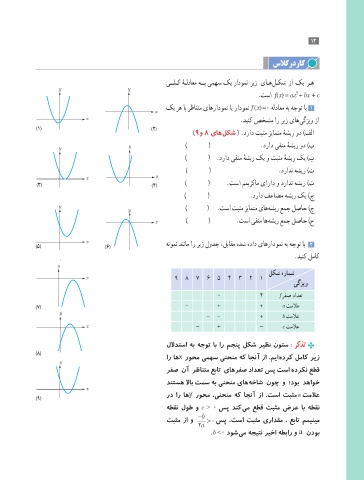
y یــلـک هـلداعم هــب یمهس کی رادومن ریز یاـه لـکش زا کی رـه
x ٔ
y x y
2
.تسا f (x) = ax + bx + c
y y x
x x کی ره اب رظانتم یاهرادومن ای رادومن f (x) =0 هلداعم هب هجوت اب 1
y y
x .دینک صخشم ار ریز یاه یگژیو زا
x
)1( y )2( x
ٔ
y (9و ٨ یاه لکش ) .دراد تبثم زیامتم هشیر ود (فلا
y
x y x ( ) .دراد یفنم هشیر ود (ب
ٔ
y
x x ( ) .دراد یفنم هشیر کی و تبثم هشیر کی (پ
y y ٔ ٔ
x
y ( ) .درادن هشیر (ت
x x
y ( ) .تسا ممیزکام یاراد و درادن هشیر (ث
)3( y )4(
x y
y x ( ) .دراد فعاضم هشیر کی ( ج
y x ( ) .تسا تبثم زیامتم یاه هشیر عمج لصاح ( چ
x y x
y x ( ) .تسا یفنم اه هشیر عمج لصاح ( ح
x x
y y
x
y x y
)5( )6( هنومن دننام ار ریز لودج ،لباقم هدش هداد یاهرادومن هب هجوت اب 2
x
y y .دینک لماک
x
y x x x
y x لکش هرامش
x y 9 8 7 6 5 4 3 2 1
y یگژیو
y x
x 0 2 f رفص دادعت
y x y
)7( x - + + a تملاع
y x
x - - + b تملاع
y y
x - + - c تملاع
y x y x
x x للادتسا هب هجوت اب ار مجنپ لکش ریظن نوتس :رکذت
y
)٨( y ار اهx روحم یمهس ینحنم هک اجنآ زا .میا هدرک لماک ریز
y x
y
y رفص نآ رظانتم عبات یاهرفص دادعت سپ تسا هدرکن عطق
y x y x x دنتسه لااب تمس هب ینحنم یاه هخاش نوچ و ؛دوب دهاوخ
x
x رد ار اهy روحم ،ینحنم هک اجنآ زا .تسا تبثم aتملاع
)9( y
x هطقن لوط و c < 0 سپ دنک یم عطق تبثم ضرع اب هطقن
y b −
y تبثم زا و >0 سپ . تسا تبثم یرادقم ، عبات ممینیم
x a 2
y x
. b >0 دوش یم هجیتن ریخا هطبار و a ندوب
x
x
y

x