Page 35 - C111214

27 هلداعم و ربج : لوا لصف

تیلاعف

2
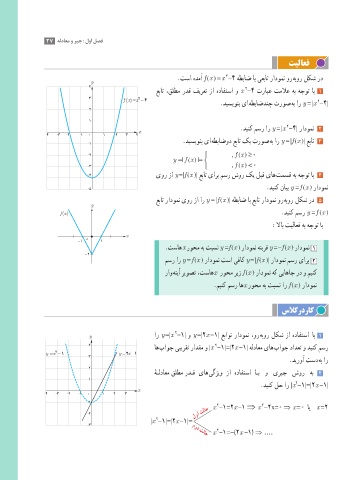
.تسا هدمآ f )x ) = x -4 هطباض اب یعبات رادومن ور هبور لکش رد
y
4 2
عبات ،قلطم ردق فیرعت زا هدافتسا و x -4 ترابع تملاع هب هجوت اب 1
3 2
x
f (x)= −4 2
.دیسیونب یا هطباضدنچ تروص هب ار y = |x -4|
2
1
2
.دینک مسر ار y = |x -4| رادومن 2
x
-4 -3 -2 -1 0 1 2 3 4
.دیسیونب یا هطباضود عبات کی تروص هب ار y = |f )x (| عبات 3
-1
x
f
-2  , ) ( ≥0
y = | ) ( |= 
f
x
f
x
-3  , ) ( <0
-4 یور زا y =|f )x (| عبات یارب مسر شور کی لبق یاه تمسق هب هجوت اب 4
-5 .دینک نایب y = f )x ( رادومن
عبات رادومن یور زا ار y = |f )x (| هطباض اب عبات رادومن ور هبور لکش رد 5
y y
fx .دینک مسر y = f )x (
()
:لااب تیلاعف هب هجوت اب
1
x x
o o
− 1 1
−
1
.تساه x روحم هب تبسن y =f )x ( رادومن هنیرق y = -f )x ( رادومن 1
− 2
مسر ار y = f )x ( رادومن تسا یفاک y = |f )x (| رادومن مسر یارب 2

راو هنیآ ریوصت ،تساهx روحم ریز f )x ( رادومن هک ییاهاج رد و مینک
.مینک مسر اهx روحم هب تبسن ار f )x ( رادومن
سلاکردراک

2
y ار y =|x -1| و y =|2x -1| عباوت رادومن ،ور هبور لکش زا هدافتسا اب 1
2
4 اه باوج یبیرقت رادقم و |x -1|=|2x -1| هلداعم یاه باوج دادعت و دینک مسر
2
x
y = −1 y = x 12 −
3
.دیروآ تسد هب ار
2
ٔ
هـلداعم قلطم ردـق یاه یگژیو زا هدافتسا اـب و یربج شور هب 2
1
2
.دینک لح ار |x -1|=|2x -1|
x
-4 -3 -2 -1 0 1 2 3
-1
2
2
x -1=2x -1 ⇒ x -2x=0 ⇒ x =0 ای x =2
-2 لوا تلاح
2
|x -1|=|2x -1|=
-3
2
مود تلاح x -1=-)2x -1( ⇒ ....