Page 41 - C111214

33 هلداعم و ربج : لوا لصف

طخ کی زا هطقن کی هلصاف

A هطقن هلصاف ،دشاب هدش هداد نآ جراخ رد A هطقن و d طخ رگا
A
هب هجوت اب .مینک یم فیرعت d زا A هلصاف نیرت هاتوک نامه ار d طخ زا
دومع ار هلصاف نیا )؟ارچ( تسا رت هاتوک لیام لوط زا دومع لوط هکنآ

.میریگ یم رظن رد AH
نآ زا تسا یفاک طخ زا هطقن ره هلصاف ندروآ تسد هب یارب نیاربانب
d
M H یریگ هزادنا ار هدش دومع طخ هراپ لوط و مسر یدومع طخ رب هطقن
.مینک

تیلاعف

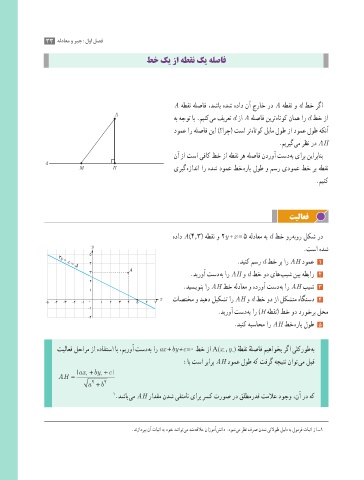
هداد A)4, 3 ( هطقن و 2y + x = 5 هلداعم هب d طخ ور هبور لکش رد
y
.تسا هدش
5
2y +
x = 4 .دینک مسر d طخ رب ار AH دومع 1
5
A
3
.دیروآ تسد هب ار AH و d طخ ود یاه بیش نیب هطبار 2
2
.دیسیونب ار AH طخ هلداعم و هدروآ تسد هب ار AH بیش 3
1
x تاصتخم و دیهد لیکشت ار AH و d طخ ود زا لکشتم هاگتسد 4
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
-1
.دیروآ تسد هب ار )H هطقن( طخ ود دروخرب لحم
-2
.دینک هبساحم ار AH طخ هراپ لوط 5

تیلاعف لحارم زا هدافتسا اب ،میروآ تسد هب ار ax + by +c =0 طخ زا A)x , y ( هطقن هلصاف میهاوخب رگا یلکروط هب
0 ٔ
ٔ
0
:اب تسا ربارب AH دومع لوط هک تفرگ هجیتن ناوت یم لبق
|ax + by + | c
AH = 0 0
2
a + b 2
1 .دشاب یم AH رادقم ندش یفنمان یارب رسک تروص رد قلطمردق تملاع دوجو ،نآ رد هک

.دنزادرپب نآ تابثا هب دوخ دنناوت یم دنم هقلاع نازومآ شناد .دوش یم رظن فرص ندش ینلاوط لیلد هب لومرف تابثا زا ــ1