Page 55 - C111214

47 عبات : مود لصف

f
x
هعومجم ربارب (( = 3 x −5 عبات هنماد :لاثم
ٔ
5 14 5 __
x 2 3 4 x ≤ ای و 3x - 5 ≤ 0 اهنآ یارب هک تسا یدادعا همه
3 3 3
5 __
. D f = ] , + ∞( :سپ
f (x( 0 1 2 7 3 3
تسا یفنم ان دادعا هعومجم زین عبات نیا درب
y R f = ]0 , + ∞( :ینعی
6
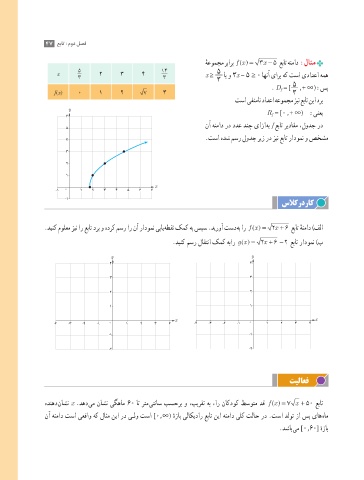
نآ هنماد رد ددع دنچ یازا هب f عبات ریداقم ،لودج رد
5
.تسا هدش مسر لودج ریز رد زین عبات رادومن و صخشم
4
3
2
1
x
-1 0 1 2 3 4 5 6 7
-1
سلاکردراک

.دینک مولعم زین ار عبات درب و هدرک مسر ار نآ رادومن یبای هطقن کمک هب سپس .دیروآ تسد هب ار (( =f x x 2 +6 عبات هنماد )فلا
ٔ
.دینک مسر لاقتنا کمک هبار (( = 2gx x +6 −2 عبات رادومن )ب

y y
4 4

3 3

2 2

1 1
x x
-4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4
-1 -1

-2 -2

تیلاعف

هدنهد ناشن x .دهد یم ناشن یگهام 60 ات رتم یتناس بسحرب و ،بیرقت هب ،ار ناکدوک طسوتم دق (( = 7 x + 50 عبات
f
x
نآ هنماد تسا یعقاو هک لاثم نیا رد یـلو تسا ]0 , ∞( هزاب یلاکیدار عبات نیا هنماد یلک تلاح رد .تسا دلوت زا سپ یاه هام
ٔ
.دشاب یم ]0 , 60[ هزاب
ٔ