Page 65 - C111214

57 عبات : مود لصف

سلاکردراک

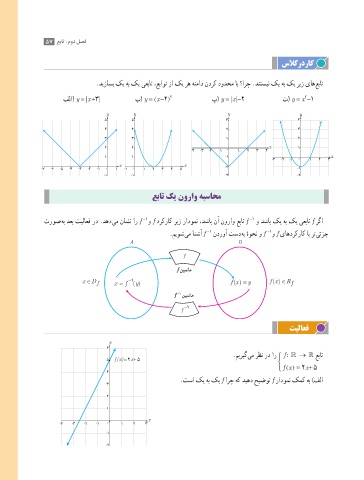
.دیزاسب کی هب کی یعبات ،عباوت زا کی ره هنماد ندرک دودحم اب ؟ارچ .دنتسین کی هب کی ریز یاه عبات

فلا( y = |x +3| ب( y = (x -2) 2 پ( y = |x |-2 ت( y = x -1
2
y y y y
5 5 3 4
4 4 2 3
3 3 1 2
2 2 x 1
-4 -3 -2 -1 0 1 2 3 4
1 1 -1 x
-3 -2 -1 0 1 2 3
x x -2
-7 -6 -5 -4 -3 -2 -1 0 1 -1 0 1 2 3 4 5 -1
-1 -1 -3 -2

عبات کی نوراو هبساحم

-1
-1
تروص هب دعب تیلاعف رد .دهد یم ناشن ار f و f درکراک ریز رادومن ،دشاب نآ نوراو عبات f و دشاب کی هب کی یعبات f رگا
-1
.میوش یم انشآ f ندروآ تسد هب هوحن و f و f یاهدرکراک اب رت یئزج
-1
ٔ
A B
f
f نیشام
∈
x D f x = f −1 () fx y f(x) R f
∈
() =
y
-1
f نیشام
−1
f
تیلاعف

y
6
.میریگ یم رظن رد ار f :  →  عبات


5 f(x)=2 x+ 5
 f (x ) = 2x + 5
4
.تسا کی هب کی f ارچ هک دیهد حیضوت f رادومن کمک هب )فلا
3
2

1
x
-4 -3 -2 -1 0 1 2 3
-1
-2