Page 69 - C111214

61 عبات : مود لصف

y
2
6 کی هب کی عبات نیا هک دهد یم ناشن g ( x ) = x -2x +3 عبات رادومن :لاثم
یعبات و درک دودحم ار عبات نیا هنماد ناوت یم .g (0) = g (2) لاثم روط هب .تسین
5
g .درک باسح ار نآ نوراو سپس و دروآ تسد هب کی هب کی
4
:میراد g عبات دروم رد
3
g :  →  D g=  و R g = ]2 , +∞)
2 2 2
( ,) g (x ) = x -2x +3 = (x -1) +2
12
1
x
-2 -1 0 1 2 3
.میمان یم f ار دیدج عبات و مینک یم دودحم ]1 , + ∞) هزاب هب ار f هنماد
ٔ
-1
.تسا ریذپ نوراو و کی هب کی عبات هک دوب دهاوخ ریز تروص هب دیدج عبات نیاربانب

)
1
f :[ ,+∞ →  D f = ]1 , + ∞) , R f = ]2 , + ∞)


2
=
x
x
  f () ( −1 ) +2
:میروآ تسد هب y بسحرب ار x مینک یم یعس نونکا
2
2
2
y = (x -1) +2 ⇒ y -2 = (x -1) ⇒ (x -1) = y -2⇒ x -1= ± y −2
:نیاربانب )؟ارچ( تسین لوبق لباق یفنم باوج
x −= y −2 ⇒ x = y −+21 ⇒ f −1 () = x −+21
1
x

:میراد تقیقح رد
∞→ 
 f −1 :[ , )
2


 D -1 = ]2 , + ∞) R -1= ]1 , + ∞)
f
f
21
x
  f −1 () = x −+
y -1
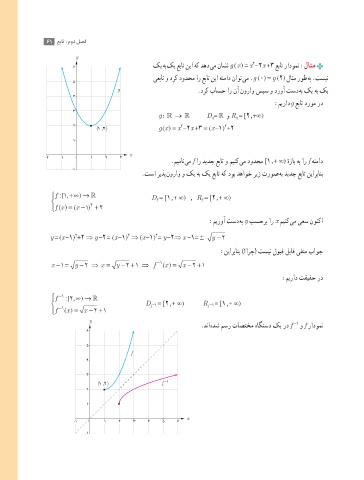
.دنا هدش مسر تاصتخم هاگتسد کی رد f و f رادومن
6
5
f
4
3
12
( ,) f −1
2
1

x
-1 0 1 2 3 4 5 6
-1