Page 73 - C111214

65 عبات : مود لصف

f x +2
هنماد و دینک هبساحم ار و g h ، g -h ، f +g عباوت ()hx = 2 x +1 و ()gx = 3 − x و f () = x +2 رگا :لاثم
x
ٔ
g
؟دنراد دوجو ( f + g) (5) و ( f + g) (2) ریداقم زا کی مادک .دیروآ تسد هب ار اهنآ

:میروآ یم تسد هب ار عباوت زا کیره هنماد ادتبا :لح
 1 
D =  −−  D = (- ∞,3] D = [-2, ∞)

h
f
g
 2 
.درادن دوجو ( f + g) (5) یلو ( f + g) (2) = 3
[
()
+
(f + g )() = f () gx = x ++ 3 − x D fg = D f D g =−2 ,]
2
x
3
x
+
x +2 1
−
3
( . )() = g ()() ( 3x h x = −x )( ) D = D D = (−∞ ,] {− }
gh x
.

2x +1 gh g h 2
x +2
(g h x = () hx = 3 − x − 1 1
−
)() g x −
()
,
3
2 x +1 D gh = D  g D = (−∞ − 2 )  (− 2 ,]
−
h
f f () x x +2
( )( ) x = = D = D  D − , ]−
3
g gx 3 − x f f g { | ()x gx =0 } [=−2 { } 3
()
g
D g
3
D h
− 1
2
تیلاعف
y
10
f+g
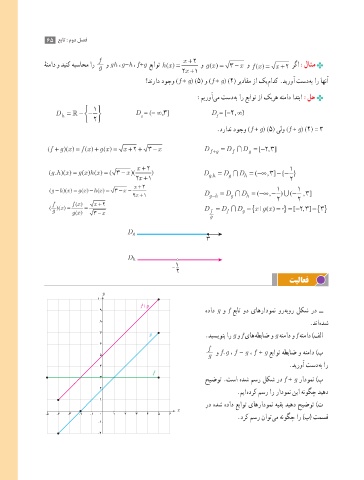
9 هداد g و f عبات ود یاهرادومن ور هبور لکش رد ــ
8 .دنا هدش
7 g .دیسیونب ار g و f یاه هطباض و g هنماد و f هنماد )فلا
6
f و f.g ، f - g ، f + g عباوت هطباض و هنماد )ب
5 g
4 .دیروآ تسد هب ار
f
3
حیضوت .تسا هدش مسر لکش رد f + g رادومن )پ
2
.میا هدرک مسر ار رادومن نیا هنوگچ دیهد
1
رد هدش هداد عباوت یاهرادومن هیقب دیهد حیضوت )ت
x
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
.درک مسر ناوت یم هنوگچ ار )ب) تمسق
-1
-2