Page 75 - C111214

67 عبات : مود لصف

:داد شیامن ناوت یم مه ریز تروص هب ار لبق هحفص یاهرادومن

f g

x f (x) g(f(x))

5 :میراد ؟درک هبساحم ناوت یم هنوگچ ار g ( f (x)) اما
fx
x
g ( ( )) = g ( ( − 32 ))
9
5 :سپ .دنک یم هفاضا دحاو 273 یدورو ره هب g عبات میناد یم و
x
fx
g ( ( )) = ( − 32 ) +273
9
)فاوا یج دیناوخب( gof اب نآ هبساحم هویش لیلد هب و دنک یم لیدبت نیولک هب ار تیاهنراف هجرد هک تسا دیدج عبات کی نیا
ٔ
.دنک یم لیدبت g ( f (x)) هب ار x یدورو هک دنک یم لمع ینیشام دننامه زین gof تقیقح رد .دوش یم هداد شیامن

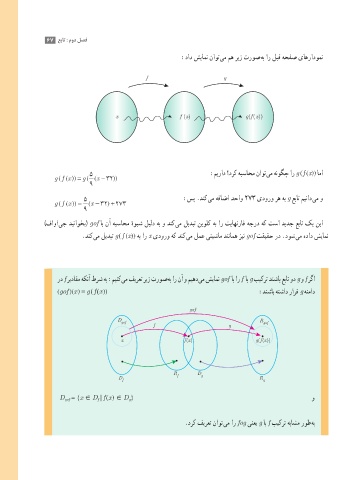
رد f ریداقم هکنآ طرش هب :مینک یم فیرعت ریز تروص هب ار نآ و میهد یم شیامن gof اب ار f اب g بیکرت دنشاب عبات ود g و f رگا
(gof )(x ) = g ( f (x )) :دنشاب هتشاد رارق g هنماد

gof
D gof R gof
f g

(
(
x fx() gf x))

R f D g
D f R g

D gof = {x ∈ D f | f (x ) ∈ D g} و

.درک فیرعت ناوت یم ار fog ینعی g اب f بیکرت هباشم روط هب