Page 82 - C111214
P. 82
74
دینک صخشم یجنرطش هحفص کی رد ار هدمآ تسد هب طاقن )ب
ٔ
.)دنا هدش صخشم هاگتسد رد طاقن زا یخرب(
y
یندناوخ 9
2 8
x y رد تابساحم مجح شیازفا لیلد هب 7
هب هتشذگ زا شیب ،هرمزور یگدنز
6
( هبساحم یارب .میدنمزاین باسح نیشام
:میهد یم ماجنا ار ور هبور لحارم 2 2 5
2
4
و 3 + 1 2 ، 3 5 ،2 ریداقم نونکا
0/5
هدافتسا اب راشعا مقر ود ات ار 3 − 1 5 3
) .دیروآ تسد هب باسح نیشام زا 2
=
1
2/6 x
-4 -3 -2 -1 0 1 2 3 4
-1
x
یقیقح دادعا همه y = 2 عبات هنماد دوش یم هظحلام هک روط نامه
ٔ
ٔ
y
.تسا تبثم دادعا هراومه نآ درب و
9 x
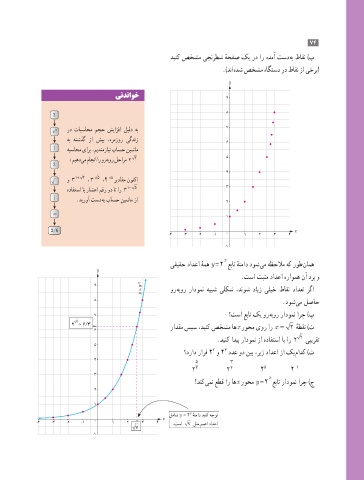
= 2 ور هبور رادومن هیبش یلکش ،دنوش دایز یلیخ طاقن دادعت رگا
y
8 .دوش یم لصاح
7 ؟تسا عبات کی ور هبور رادومن ارچ )پ
7
2 6/3
ٔ
6 رادقم سپس ،دینک صخشم اه x روحم یور ار = 2x هطقن )ت
2
.دینک ادیپ رادومن زا هدافتسا اب ار 2 یبیرقت
5
2
3
؟دراد رارق 2 و 2 ددع ود نیب ،ریز دادعا زا کی مادک )ث
4
5 3
5
2
2
2 2 2 2 -1
3 x
؟دنک یمن عطق ار اهx روحم y = 2 عبات رادومن ارچ )ج
2
1
x
لماش y = 2 هنماد دینک هجوت
ٔ
x
-4 -3 -2 -1 0 1 2 3 4 .تسا 7 لثم مصا دادعا
7
-1