Page 88 - C111214

2

متیراگل و یمتیراگل عبات

سرد
سرد

حرطم لصف نیا یادتبا رد هک ار تشک طیحم رد یرتکاب هدوت مرج شیازفا هلئسم ،رگید راب

رگا ینعی ،تسا مرگ 512 اه یرتکاب نزو ینامز هچ رد مینادب میهاوخ یم .دیریگب رظن رد ،دش
t
سپ ،تسا کی هب کی عبات کی m (t ( = 2 عبات نوچ .میبایب ار t میهاوخ یم ،m (t ( = 512 یندناوخ
-1
:دینک هاگن ریز یاه لودج هب .t = m (512( ور نیا زا و تسا ریذپ نوراو ) John Napier ( رپن ناج
موهفم یدنلتاکسا نادیضایر رپن ناج
یارب متیراگل .درک یزیر هیاپ ار متیراگل
-1
)نامز( t t نامز رد اه یرتکاب مرج ،m )t( = p p مرج هب ندیسر نامز ،m )p( )نامز( t
رد و دش عادبا تابساحم ندرک هداس
0 1 1 0 رد تفرشیپ نیرت گرزب 17و 16 نرق
یدایز مولع رد متیراگل .دوب باسح ملع
1 2 2 1 یارب یسانش هلزلز رد ً لاثم .دراد دربراک
رتشیر بسحرب هلزلز تدش یریگ هزادنا
2 4 ⇒ 4 2 و یرادباسح رد متیراگل .دراد دربراک
.دراد یدایز یاهدربراک زین یلام لئاسم
3 8 8 3
4 16 16 4

5 32 32 5

y
6
x
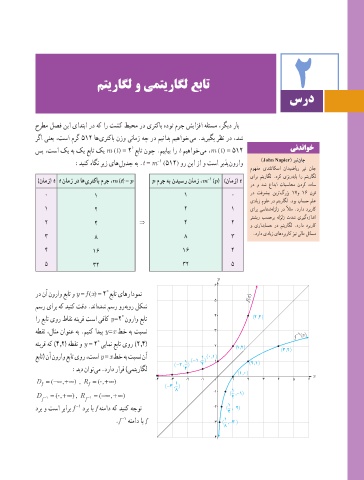
رد نآ نوراو عبات و y = f (x( = 2 عبات یاهرادومن )
5 f (x
مسر یارب هک دینک تقد .دنا هدش مسر ور هبور لکش
x
24
ار عبات یور طاقن هنیرق تسا یفاک y = 2 نوراو عبات 4 (, )
هطقن ،لاثم ناونع هب .مینک ادیپ y = x طخ هب تبسن 3 −1
f ( ) x
x
هنیرق هک )4,2( هطقن و y = 2 ییامن عبات یور )2,4( 2
12
(, )
(, )
4 2
عبات( نآ نوراو عبات یور ،تسا y = x طخ هب تبسن نآ 1 (, )
0 1
1 (−1 ,) 1 (, )
2 1
(−2 ,) 2
:دید ناوت یم .دراد رارق )یمتیراگل 4
1 0
(, ) x
D = (−∞ +∞ ( , R = ( ,+∞ ( -4 -3 1 -2 -1 0 1 2 3 4 5 6
,

0
f
f
(−3 ,)
8 -1 1
D − = ( ,+∞ 1 ( , ( (,−1 )
( , R − = −∞ +∞
0
2
1
f f
1
-1
درب و تسا ربارب f درب اب f هنماد هک دینک هجوت -2 (,−2 )
4
1
.f هنماد اب f -3 (,−3 )
-1
8
-4