Page 89 - C111214

81 متیراگل و ییامن عباوت : موس لصف

تیلاعف

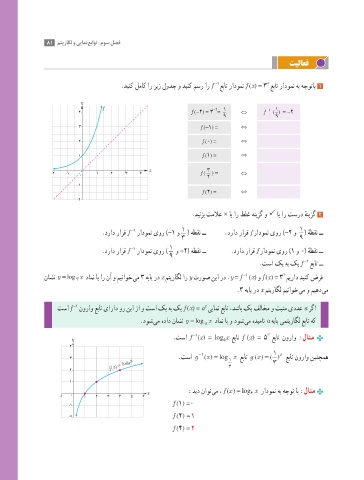
-1 x
.دینک لماک ار ریز لودج و دینک مسر ار f عبات رادومن f (x( = 3 عبات رادومن هب هجوتاب 1

y
f -2 1 -1 1
4 f (-2( = 3 = ⇔ f (( = -2
9 9
3 f (-1( = ⇔

2 f (0( = ⇔

1 f (1( = ⇔
x 3
-2 -1 1 2 3 4 f ( ( = ⇔
0 2
-1
f (2( = ⇔
-2

.دینزب تملاع × اب ار طلغ هنیزگ و  اب ار تسرد هنیزگ 2
ٔ
1
1
-1
.دراد رارق f رادومن یور )-1 و ( هطقن ــ .دراد رارق f رادومن یور )-2 و ( هطقن ــ
ٔ
3 9
1
-1
.دراد رارق f رادومن یور ) و -2( هطقن ــ .دراد رارق f رادومن یور )1 و 0( هطقن ــ
9 ٔ
-1
.تسا کی هب کی f عبات ــ
x
ناشن =y log x دامن اب ار نآ و میناوخ یم 3 هیاپ رد x متیراگل ار y تروص نیا رد .y = f (x( و f (x( = 3 میراد دینک ضرف
-1
3
.3 هیاپ رد x متیراگل میناوخ یم و میهد یم
x
تسا f نوراو عبات یاراد ور نیا زا و تسا کی هب کی f (x( = a ییامن عبات ،دشاب کی فلاخم و تبثم یددع a رگا
-1
.دوش یم هداد ناشن y = log x دامن اب و دوش یم هدیمان a هیاپ یمتیراگل عبات هک
a
x
-1
y .تسا f (x( = log x عبات f (x( = 5 عبات نوراو :لاثم
y 5
4
4
1
x
=
=
gx
x
3 .تسا g −1 ( ( log x عبات (( ( ( عبات نوراو نینچمه
3 log x 1 3
2 f x ( ) = 2 3
2
1
1
x :دید ناوت یم ، ( ( log=f x x رادومن هب هجوت اب :لاثم
-1 0 1 2 3 4 5 6 7 8 9 10 x 2
-1 0 1 2 3 4 5 6
-1 f (1( =0
-1
-2
-2 f (2( = 1
-3
f (4( = 2