Page 104 - C111211

تاثلثم 4 لصف

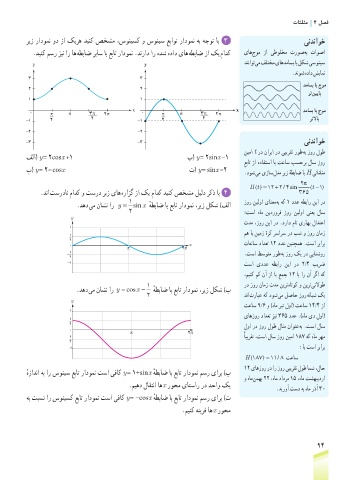
ریز رادومن ود زا کیره دینک صخشم ،سونیسک و سونیس عباوت رادومن هب هجوت اب 3 یندناوخ

.دینک مسر زین ار اه هطباض ریاس اب عبات رادومن .دنراد ار هدش هداد یاه هطباض زا کی مادک یاه جوم زا یطولخم تروص هب تاوصا
y y دنناوت یم فلتخم یاهدماسب اب لکش یسونیس
.دنوش هداد شیامن
3 3
دماسب اب جوم
2 2
رت نییاپ
1 1
x x
0 π π 3 π 2 π 0 π π 3 π 2 π دماسب اب جوم
1 − 2 2 1 − 2 2 رتلااب

2 − 2 −
3 − 3 − یندناوخ
نیما t رد ناریا رد یبیرقت روط هب زور لوط
فلا( y = 2cosx +1 ب( y = 2sinx -1
عبات زا هدافتسا اب تعاس بسح رب لاس زور
پ( y = 2- cosx ت( y = sinx -2 .دوش یم یزاس لدم ریز هطباض اب H یتاثلثم
ٔ
2 π
+
H ) ( =12 2 / sin ) −1 (
t
4
t
.دنا تسردان مادک و تسرد ریز یاه هرازگ زا کی مادک دینک صخشم لیلد رکذ اب 4 365
1 زور نیلوا یانعم هب هک 1 ددع هطبار نیا رد
.دهد یم ناشن ار y = sinx ٔهطباض اب عبات رادومن ،ریز لکش )فلا
2 ؛تسا هام نیدرورف زور نیلوا ینعی لاس
y
تدم ،زور نیا رد .دراد مان یراهب لادتعا
1
مه اب نیمز هرک رسارس رد بش و زور نامز
1 ٔ
2
0 π 2 π x تاعاس دادعت 12 ددع نینچمه .تسا ربارب
− 1 .تسا طسوتم روط هب زور کی رد ییانشور
2
−1 تسا یددع هطبار نیا رد 2/4 بیرض
،مینک مک نآ زا ای عمج 12 اب ار نآ رگا هک
1 رد زور نامز تدم نیرت هاتوک و نیرت ینلاوط
.دهد یم ناشن ار = cos − ٔهطباض اب عبات رادومن ،ریز لکش )ب
y
x
2 دنا ترابع هک دوش یم لصاح زور هنابش کی
y
تعاس 9/6 و )هام ریت لوا( تعاس 14/4 زا
1
یاهزور دادعت زین 365 ددع .)هام ید لوا(
1
2 لوا رد زور لوط لاثم ناونع هب .تسا لاس
0 π 2 π
− 1 ًابیرقت ،تسا لاس زور نیما 187 هک هام رهم
2
-1 :اب تسا ربارب
/

H )187 ( 11 8 تعاس
12 یاهزور رد ار زور یبیرقت لوط امش ،لاح
هزادنا هب ار سونیس عبات رادومن تسا یفاک y = 1+sin x ٔهطباض اب عبات رادومن مسر یارب )پ
ٔ
و هام نمهب 22 ،هام دادرم 15 ،هام تشهبیدرا
.میهد لاقتنا اه x روحم یاتسار رد دحاو کی
.دیروآ تسد هب هام رذآ 30
هب تبسن ار سونیسک عبات رادومن تسا یفاک y = -cosx ٔهطباض اب عبات رادومن مسر یارب )ت
.مینک هنیرق اه x روحم

9٤