Page 119 - C111211

نآ یاه یگژیو و یمتیراگل عبات مود سرد

تیلاعف

.دینک لیمکت ار ریز تلامج ،دیا هدناوخ لاح هب ات هک یبلاطم هب هجوت اب

.تسا .............. نآ درب و تبثم یقیقح دادعا هعومجم،(a >1)y = log x هطباض اب عبات هنماد 1
a ٔ
ٔ
ٔ
.تسا .............. نآ درب و .............. هزاب ،(0< a <1)y = log x هطباض اب عبات هنماد 2
ٔ
a ٔ
.دنک یمن عطق ار اهy روحم و دنک یم عطق .............. هطقن رد ار اهx روحم ،قوف عباوت رادومن 3
ٔ
.دنک یم عطق هطقن .............. رد رثکادح ار اهنآ رادومن ،اهx روحم یزاوم طوطخ اریز .............. کی هب کی ،عبات ود نیا 4
.تسا .............. عبات ،یمتیراگل عبات نوراو و تسا .............. عبات ،ییامن عبات نوراو 5

:هراومه نیاربانب ،a =1 :میراد ،دشاب (a ≠1( تبثم یقیقح ددع a رگا
0
log 1 = 0
a

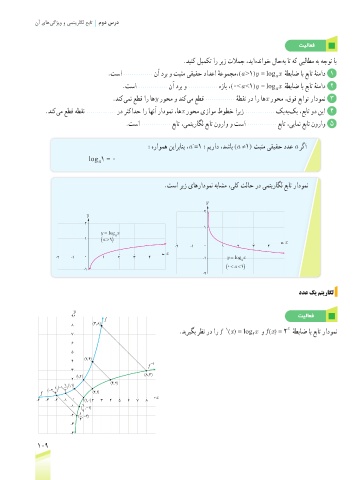
.تسا ریز یاهرادومن هباشم ،یلک تلاح رد یمتیراگل عبات رادومن

y
2
y
2
1
y = log x
a
1 (a >1 ) x
-2 -1 0 1 2 3 4
x
-2 -1 0 1 2 3 4 -1 y = log x
a
( < <0 a ) 1
-1
-2

ددع کی متیراگل

y
9 تیلاعف
f
38
8 (, ) x
.دیریگب رظن رد ار f (x) = log x و f (x) = 2 هطباض اب عبات رادومن
-1
7 2 ٔ
6
5
24
(, )
4 −1
f
3
83
(, ) (, )
12
2
4 2
(, )
01
1
−
1
1 ( ,) (, )
(−2 ,) 2 1
21
f 4 (, )
-4 -3 -2 -1 0 1(, )10 2 3 4 5 6 7 8 x
1
-1 (,−1 )
2
1
-2 (,−2 )
4
-3
-4
109