Page 133 - C111211

یدح یاهدنیارف لوا سرد

+
-
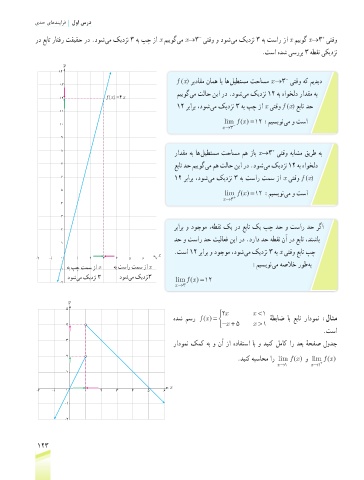
رد عبات راتفر تقیقح رد .دوش یم کیدزن 3 هب پچ زا x مییوگ یم x→3 یتقو و دوش یم کیدزن 3 هب تسار زا x مییوگ x→3 یتقو
.تسا هدش یسررب 3 هطقن یکیدزن
y
14
f (x) ریداقم نامه ای اه لیطتسم تحاسم x →3 یتقو هک میدید
-
13
مییوگ یم تلاح نیا رد .دوش یم کیدزن 12 هب هاوخلد رادقم هب
12 f (x) =4 x
12 ربارب ،دوش یم کیدزن 3 هب پچ زا x یتقو f (x) عبات دح
11
lim f (( =12 :میسیون یم و تسا
x
10 −
x →3
9

8 +
رادقم هب اه لیطتسم تحاسم مه زاب x→3 یتقو هباشم قیرط هب
7
عبات دح مییوگ یم مه تلاح نیا رد .دوش یم کیدزن 12 هب هاوخلد
12 ربارب ،دوش یم کیدزن 3 هب تسار تمس زا x یتقو f (x)
6

5
x
lim f (( =12 :میسیون یم و تسا
x →3 +
4
3
ربارب و دوجوم ،هطقن کی رد عبات کی پچ دح و تسار دح رگا
2
دح و تسار دح تیلاعف نیا رد .دراد دح هطقن نآ رد عبات ،دنشاب
1
.تسا 12 ربارب و دوجوم ،دوش یم کیدزن 3 هب x یتقو عبات پچ
x
-2 -1 0 1 2 3 4 5 6 7
-1 هب پچ تمس زا x هب تسار تمس زا x :میسیون یم هصلاخ روط هب
دوش یم کیدزن 3 دوش یم کیدزن3 lim f (( =12
x
-2
x →3
y
5
2 x x <1
x
f
هدش مسر (( =  هطباض اب عبات رادومن :لاثم
ٔ
4  x −+ 5 x >1
.تسا
3
رادومن کمک هب و نآ زا هدافتسا اب و دینک لماک ار دعب هحفص لودج
ٔ
2
x
x
.دینک هبساحم ار lim f (( و lim f ((
x →1 − x →1 +
1
x
-2 -1 0 1 2 3 4 5 6
-1

-2

1٢3