Page 134 - C111211

یگتسویپ و دح ٦ لصف

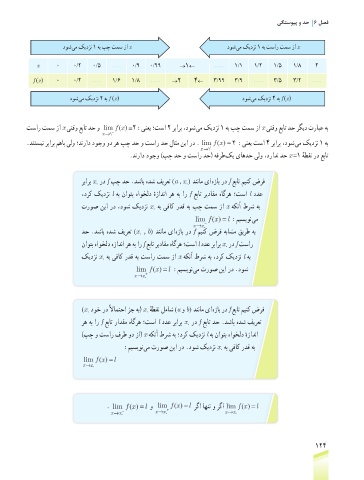
دوش یم کیدزن 1 هب پچ تمس زا x دوش یم کیدزن 1 هب تسار تمس زا x

x ٠ ٠/٢ ٠/5 .... ٠/9 ٠/99 →1← .... 1/1 1/٢ 1/5 1/8 ٢

f (x) ٠ ٠/٤ .... 1/6 1/8 .... →٢ ٤← 3/99 3/9 .... 3/5 3/٢ ....

دوش یم کیدزن ٢ هب f (x) دوش یم کیدزن ٤ هب f (x)

x =
تسار تمس زا x یتقو عبات دح و lim f (( = 2 :ینعی ؛تسا 2 ربارب ،دوش یم کیدزن 1 هب پچ تمس زا x یتقو عبات دح رگید ترابع هب
2
x →1 −
x
.دنتسین ربارب مهاب یلو ؛دنراد دوجو ود ره پچ دح و تسار دح لاثم نیا رد . lim f (( = 4 :ینعی تسا 4 ربارب ،دوش یم کیدزن 1 هب
x →1 +
.دنراد دوجو )پچ دح و تسار دح( هفرط کی یاهدح یلو ،درادن دح x =1 هطقن رد عبات
ٔ
ربارب x رد f پچ دح .دشاب هدش فیرعت (a , x ( دننام یا هزاب رد f عبات مینک ضرف
0 0
،درک کیدزن l هب ناوتب هاوخلد هزادنا ره هب ار f عبات ریداقم هاگره ؛تسا l ددع
ٔ
تروص نیا رد ،دوش کیدزن x هب یفاک ردق هب پچ تمس زا x هکنآ طرش هب
0
x
lim f (( =l :میسیون یم
x →x 0 −
دح .دشاب هدش فیرعت (x , b( دننام یا هزاب رد f مینک ضرف هباشم قیرط هب
0
ناوتب هاوخلد هزادنا ره هب ار f عبات ریداقم هاگره ؛تسا l ددع ربارب x رد f تسار
0
کیدزن x هب یفاک ردق هب تسار تمس زا x هکنآ طرش هب ،درک کیدزن l هب
0
lim f (( =l :میسیون یم تروص نیا رد .دوش
x
x →x 0 +

(x دوخ رد لاامتحا زج هب( x هطقن لماش (a و b( دننام یا هزاب رد f عبات مینک ضرف
0 ً 0 ٔ
ره هب ار f عبات رادقم هاگره ؛تسا l ددع ربارب x رد f عبات دح .دشاب هدش فیرعت
0
)پچ و تسار فرط ود زا( x هکنآ طرش هب ؛درک کیدزن l هب ناوتب هاوخلد هزادنا
ٔ
:میسیون یم تروص نیا رد .دوش کیدزن x هب یفاک ردق هب
0
lim f (( =l x
x →x 0

x
x
. lim f (( =l و lim f (( =l رگا اهنت و رگا lim f (( =l
x
x →x 0 − x →x 0 + x →x 0

1٢٤