Page 135 - C111211

یدح یاهدنیارف لوا سرد

رد .مینک یسررب هطقن کی یکیدزن رد ار عبات کی راتفر تسا مزلا عقاوم زا یرایسب رد .دنا عبات کی بلاق رد هئارا لباق یعیبط یاه هدیدپ زا یرایسب

.میوش انشآ رتهب دح موهفم اب ات درک میهاوخ یسررب هطقن کی یکیدزن رد ار عبات هس راتفر ریز تیلاعف

تیلاعف

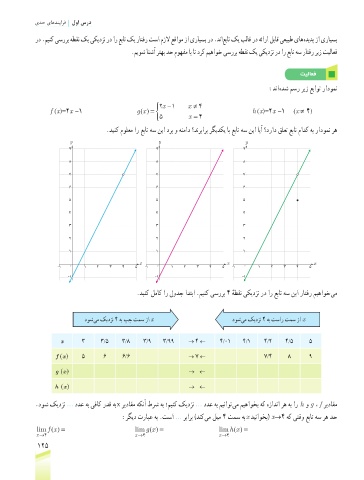
:دنا هدش مسر ریز عباوت رادومن

2 x −1 x ≠ 4
f (x)=2x -1 ((gx =  h (x)=2x -1 (x ≠ 4)
 5 x = 4

.دینک مولعم ار عبات هس نیا درب و هنماد ؟دنربارب رگیدکی اب عبات هس نیا ایآ ؟دراد قلعت عبات مادک هب رادومن ره

y y y
9 9 9

8 8 8
7 7 7

6 6 6
5 5 5

4 4 4
3 3 3

2 2 2

1 1 1
x x x
-1 0 1 2 3 4 5 -1 0 1 2 3 4 5 -1 0 1 2 3 4 5
-1 -1 -1

.دینک لماک ار لودج ادتبا .مینک یسررب 4 هطقن یکیدزن رد ار عبات هس نیا راتفر میهاوخ یم
ٔ

دوش یم کیدزن 4 هب پچ تمس زا x دوش یم کیدزن 4 هب تسار تمس زا x

x 3 3/5 3/8 3/9 3/99 → ٤ ← ٤/٠1 ٤/1 ٤/٢ ٤/5 5

f (x ) 5 6 6/6 → ٧ ← ٧/٤ 8 9

g (x ) → ←

h (x ) → ←

.دوش کیدزن … ددع هب یفاک ردق هب x ریداقم هکنآ طرش هب ؛مینک کیدزن … ددع هب میناوت یم میهاوخب هک هزادنا ره هب ار h و g ، f ریداقم
:رگید ترابع هب .تسا … ربارب )دنک یم لیم 4 تمس هب x دیناوخب( x→4 هک یتقو عبات هس ره دح

(( =
(( =
x
lim f (( = lim gx lim hx
x →4 x →4 x →4
1٢5