Page 136 - C111211

یگتسویپ و دح ٦ لصف

کیدزن 4 هب x یتقو اهنآ دح رگید ترابع هب .دنراد یناسکی راتفر x = ٤ هطقن یکیدزن رد h و g ، f عبات هس هک دیدرک هدهاشم لبق تیلاعف رد
ٔ
:میراد 4 هطقن رد عبات هس نیا ریداقم هرابرد لاح نیا اب .تسا 7 ربارب ،دوش یم
ٔ
.)تسا هدشن فیرعت 4 رد h ( درادن دوجو h (4) )فلا

4
. lim ( ( ≠ gx g ( ( یلو ؛تسا دوجوم g (4) )ب
x →4
. lim ( ( =f x 7 و f (4) = 7 )پ
x →4

=
f (a ) هرابرد هاگنآ ، lim ( ( l میشاب هتشاد f دننام یعبات هرابرد رگا یلک روط هب
f
x
ٔ
ٔ
x→
a
:میراد ار ریز یاه تلاح زا یکی
.تسین دوجوم f (a) )فلا
( ( یلو ؛تسا دوجوم f (a) )ب
. lim ( ( ≠ f x fa
x →a
. lim ( ( = f x fa
( ( )پ
x →a

-2x + 8 x > 2
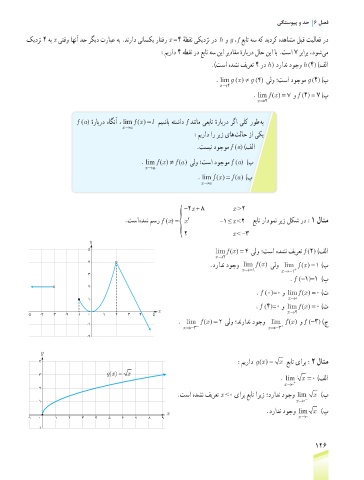
.تسا هدش مسر f (x) = x -1 ≤ x < 2 عبات رادومن ریز لکش رد :1 لاثم
2
2 x < -3
y

5 lim f (( = 4 یلو ؛تسا هدشن فیرعت f (2) )فلا
x
x →2
4
x
.درادن دوجو lim f (( یلو lim f (( =1 )ب
x
x →−1 x →−1 +
3
. f (-1)=1 )پ
2
x
. f (0)=0 و lim f (( =0 )ت
1 x →0
x
. f (4)=0 و lim f (( =0 )ث
x x →4
-5 -4 -3 -2 -1 0 1 2 3 4 5
. lim f (( = 2 یلو ؛دنرادن دوجو lim f (( و f (-3) ) ج
x
x
-1 − +
x →−3 x →−3
-2
y
4 :میراد (( =gx x عبات یارب :2 لاثم
g(x) = x
3
. lim x =0 )فلا
x →0 +
2
.تسا هدشن فیرعت x <0 یارب عبات اریز ؛درادن دوجو lim x ) ب
1 x →0 −
x .درادن دوجو lim x ) پ
-1 0 1 2 3 4 5 6 7 8 9 x →0
-1

1٢6