Page 137 - C111211

یدح یاهدنیارف لوا سرد

نیرتم

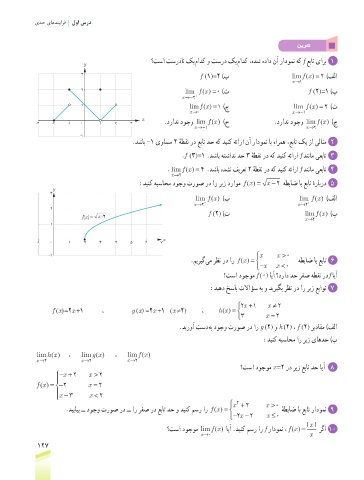
؟تسا تسردان کی مادک و تسرد کی مادک ،هدش هداد نآ رادومن هک f عبات یارب 1
y
3 f (1)=2 )ب lim f (( = 2 )فلا
x
x →1
x
lim f (( =0 )ت f (2)=1 )پ
2
x →−2 +
x
x
1 lim f (( =1 )ج lim f (( = 2 )ث
x →0 x →−1
x .درادن دوجو lim ( (f x )ح .درادن دوجو lim f (( )چ
x
-3 -2 -1 0 1 2 3
x →−1 x →2
-1
.دشاب -1 یواسم 2 هطقن رد عبات دح هک دینک هئارا نآ رادومن اب هارمه ،عبات کی زا یلاثم ٢
ٔ
.f (3)=1 .دشاب هتشادن دح 3 هطقن رد هک دینک هئارا f دننام یعبات 3
ٔ
x
. lim f (( = 4 .دشاب هدشن فیرعت 2 هطقن رد هک دینک هئارا f دننام یعبات ٤
ٔ
x →2
:دینک هبساحم دوجو تروص رد ار ریز دراوم ((f x = x −2 هطباض اب عبات هرابرد 5
y ٔ
3
lim f (( )ب lim f (( )فلا

x
x
x →2 − x →2 +
2
x
f(x) = x -2 f (2) )ت lim f (( )پ
→2
x
1
x
-1 0 1 2 3 4 5 6 7
-1 x  x >0
x
f
.میریگ یم رظن رد ار (( =  هطباض اب عبات 6
 x − x <0
؟تسا دوجوم f (0) ایآ ؟دراد دح رفص هطقن رد f ایآ
:دیهد خساپ تلااؤس هب و دیریگب رظن رد ار ریز عباوت ٧
 x 2 +1 x ≠ 2
hx
f (x( =2x +1 ، g (x) =2x +1 (x ≠2) ، (( = 
 3 x = 2
.دیروآ تسد هب دوجو تروص رد ار g (2) و h (2) ، f (2) ریداقم )فلا
:دینک هبساحم ار ریز یاهدح )ب

(( ، lim
(( ، lim
lim hx gx f ((
x
x →2 x →2 x →2
؟تسا دوجوم x =2 رد ریز عبات دح ایآ 8
 x −+2 x > 2

f (( =−2 x = 2
x


 x − 3 x < 2
 x  2 +2 x >0
f
x
.دیبایب ــ دوجو تروص رد ــ ار رفص رد عبات دح و دینک مسر ار (( =  هطباض اب عبات رادومن 9
ٔ
  −2 x −2 x ≤0
|| x
x
x
f
؟تسا دوجوم lim f (( ایآ .دینک مسر ار f رادومن ، (( = رگا 10
x →0 x
1٢٧