Page 142 - C111211

یگتسویپ و دح ٦ لصف

x 2 −4
.دینک هبساحم ار lim :لاثم
−
2
x → x 2
، lim ( x ( −2 ( = lim x 2 ( −4 =0 :میراد
x
x 2 −4 ( +2 (( −2 ( x →2 x →2
x
lim = lim ( = lim x ( +2 = 4
−
x → x 2 x →2 x −2 x →2
2
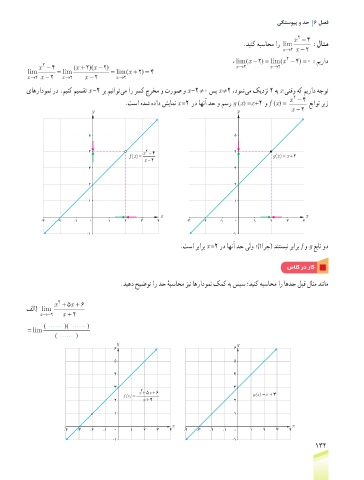
یاهرادومن رد .مینک میسقت x -2 رب میناوت یم ار رسک جرخم و تروص و x -2 ≠0 سپ x ≠2 ،دوش یم کیدزن ٢ هب x یتقو هک میراد هجوت
x 2 −4
.تسا هدش هداد شیامن x =2 رد اهنآ دح و مسر g (x) =x +2 و f (x) = عباوت ریز
y y x −2

5 5

2
4 x −4 4
=
f(x) = g(x) x +2
x −2
3 3
2 2

1 1
x x
-3 -2 -1 0 1 2 3 4 -3 -2 -1 0 1 2 3 4
-1 -1
.تسا ربارب x =2 رد اهنآ دح یلو ؛)؟ارچ( دنتسین ربارب f و g عبات ود

سلاک رد راک

.دیهد حیضوت ار دح هبساحم زین اهرادومن کمک هب سپس ؛دینک هبساحم ار اهدح لبق لاثم دننام
ٔ

+
x 2 + x 6
5
فلا( lim
x →−2 x +2
( ( (…… …… (
= lim
( …… (
yy yy
6 6 66
5 5 5 5

4 4 4 4

3 3 3 3
x + x + 22 x + 5 x + 5 66
=
=
+
g(
f(x) == g(x) x + 33
x
)
x
f(x)
x +
2 2 x +22 2 2
1 1 1 1
xx xx
-4-4 -3-3 -2-2 -1-1 0 0 11 22 33 44 -4 -4 -3 -3 -2-2 -1-1 0 0 11 22 33 44
-1 -1 -1 -1
13٢