Page 144 - C111211

یگتسویپ و دح ٦ لصف
؟دراد قلعت عبات مادک هب رادومن ره )فلا

؟دندوجوم lim gx f (( ایآ )ب
(( و lim
x
x →5 x →5
.دینک هبساحم ار اهنآ ؟دندوجوم ریز یاهدح زا کی مادک )پ
……
lim x 2 −6 = lim x 2 −6 = …… lim x 2 −6 = ……
x →3 + x →3 − x →3

.دینک یسررب ار ریز یاه هرازگ یتسردان ای یتسرد (( = || x عبات هرابرد 2
hx
x ٔ
hx
0
lim ( ( =1 )پ D h =  − {} )ب h (x)=1 )فلا
x →0 +
(( =1
.درادن دوجو lim hx )ث h (0)=0 )ت
x →0
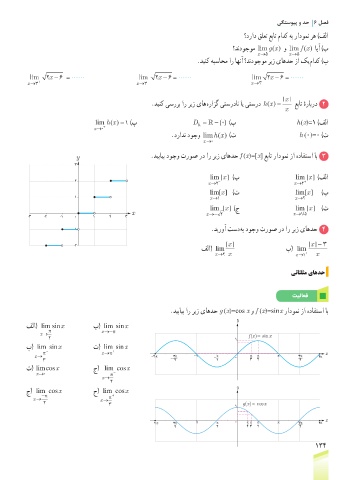
y .دیبایب دوجو تروص رد ار ریز یاهدح f (x)=[x] عبات رادومن زا هدافتسا اب 3
3
lim [ ] )ب lim [ ] )فلا
x
x
2 − +
x →2 x →2
x
x
lim[ ] )ت lim[ ] )پ
1 x →1 x →2
x
x
lim [ ] )ج lim [ ] )ث
x x →− 2 x →15
/
-3 -2 -1 0 1 2 3
-1 .دیروآ تسد هب دوجو تروص رد ار ریز یاهدح 4
x
x
فلا) lim ب) lim
-2 [] y []− 3
x → x x →1 + x
2
( )=
gx cosx
1
یتاثلثم یاهدح
−π − 3 π −π − π 0 π π π π 3 π 2π x
2
2 2 4 3 2 2
تیلاعف
.دیبایب ار ریز یاهدح g (x)=cos x و f (x)=sin x رادومن زا هدافتسا اب
y
فلا) lim sinx ب) lim sinx
x → π x →−π fx sin x
( )=
2 1
پ) lim sinx ت) lim sinx
π − x →π + x
x→ −π − 3 π −π − π 0 π π π 3 π 2π
2
3 2 2 3 2 2
ث) limcosx ج) lim cosx
x →0 π −
x→
4
y
چ) lim cosx ح) lim cosx
x→ −π x → π +
2 3 1 gx cosx
( )=
x
−π − 3 2 π −π − 2 π 0 π π 2 π π 3 2 π 2π
2
4 3
134

y

( )=
fx sin x
1
−π − 3 2 π −π − 2 π 0 π 3 2 π π 3 2 π 2π x
2