Page 148 - C111211

یگتسویپ و دح ٦ لصف

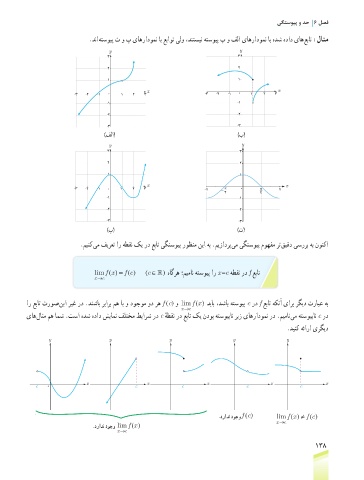
.دنا هتسویپ ت و پ یاهرادومن اب عباوت یلو ،دنتسین هتسویپ ب و فلا یاهرادومن اب هدش هداد یاه عبات :لاثم

y y y y y y y y
3 3 3 3 3 3 3 3
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1

x x x x x x x x
-3 -2 -1 0 1 -3 2 -2 3 -1 -3 0 -2 1 -1 0 2 1 3 -3 2 -2 3 -1 -3 0 -2 1 -1 2 0 3 1 -3 2 -2 3 -1 -π 0 − π1 0 2 3 -π π − π π 0 π π
2 2 2 2
-1 -1 -1 -1 -1 -1 -1 -1
-2 -2 -2 -2 -2 -2 -2 -2

-3 -3 -3 -3 -3 -3 -3 -3
)فلا( )ب(
y y y y y y y y
3 3 3 3 3 3 3 3
2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1
x x x x x x x x
-3 -2 -1 0 1 -3 2 -2 3 -1 -3 0 -2 -1 1 0 2 1 3 -3 2 -2 3 -1 -3 0 -2 1 -1 0 2 3 1 -3 2 -2 3 -π -1 0 − π 1 0 2 3 π -π − π π 0 π π
2 2 2 2
-1 -1 -1 -1 -1 -1 -1 -1
-2 -2 -2 -2 -2 -2 -2 -2

-3 -3 -3 -3 -3 -3 -3 -3
)پ( )ت(

.مینک یم فیرعت ار هطقن کی رد عبات یگتسویپ روظنم نیا هب .میزادرپ یم یگتسویپ موهفم رت قیقد یسررب هب نونکا

x
lim f ( ( = fc c 
(( ( ∈ ) هاگره ؛میمان هتسویپ ار x =c هطقن رد f عبات
x →c

x
ار عبات تروص نیا ریغ رد .دنشاب ربارب مه اب و دوجوم ود ره f (c) و lim f (( دیاب ،دشاب هتسویپ c رد f عبات هکنآ یارب رگید ترابع هب
x →c
یاه لاثم مه امش .تسا هدش هداد شیامن فلتخم طیارش رد c هطقن رد عبات کی ندوب هتسویپان ریز یاهرادومن رد .میمان یم هتسویپان c رد
ٔ
.دینک هئارا یرگید
y y y y y

x x x x x
c 0 c c c c

f (c)
((
x
.درادن دوجو lim f ( ( ≠ fc
x
.درادن دوجو lim f (( x →c
x →c
138