Page 151 - C111211

یگتسویپ موس سرد

یور f مییوگ یم ،دشاب هتسویپ شا هنماد زا هطقن ره رد f و D f =  رگا
.تسا هتسویپ (- ∞,+ ∞( هزاب
ٔ

سلاک رد راک

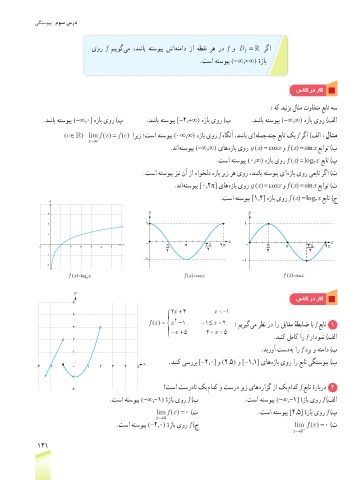
:هک دینزب لاثم توافتم عبات هس
.دشاب هتسویپ (-∞,0] هزاب یور )پ .دشاب هتسویپ [-2,+∞( هزاب یور )ب .دشاب هتسویپ (-∞,∞( هزاب یور )فلا

((
( ∈ ( lim f ( ( = fc اریز ؛تسا هتسویپ (-∞,∞( هزاب یور f هاگنآ ،دشاب یا هلمجدنچ عبات کی f رگا )فلا :لاثم
x
c
x →c
.دنا هتسویپ (-∞,∞( یاه هزاب یور g (x( = cosx و f (x( = sin x عباوت )ب
.تسا هتسویپ (0,∞( هزاب یور f (x( = log x عبات )پ
3
.تسا هتسویپ زین نآ زا هاوخلد هزاب ریز ره یور ،دشاب هتسویپ یا هزاب یور یعبات رگا )ت
.دنا هتسویپ [0,2π] یاه هزاب یور g (x( = cosx و f (x( = sin x عباوت )ث

.تسا هتسویپ [1,2] هزاب یور f (x( = log x عبات )ج
y 3
y y
3
2 1 1
1
x x
x 0 π π 3 π 2 π 0 π π 3 π π
-1 0 1 2 3 4 5 6 2 2
2 2 2
-1
1 − −1
-2
f (x)=log x f (x)=cosx f (x)=sin x
3
y
سلاک رد راک
5
2 x +4 x <- 1
4
2
f (( = x −1 - 1 ≤ x 2<
x
ٔ
3 :میریگ یم رظن رد ار لباقم هطباض اب f عبات 1
x 5
x −+5 2<<
2 .دینک لماک ار f رادومن )فلا
.دیروآ تسد هب ار f درب و هنماد )ب
1
x .دینک یسررب [-2,0] و (2,5( و [-1,1] یاه هزاب یور ار عبات یگتسویپ )پ
-3 -2 -1 0 1 2 3 4 5
-1
؟تسا تسردان کی مادک و تسرد ریز یاه هرازگ زا کی مادک f عبات هرابرد 2
-2 ٔ
.تسا هتسویپ (-∞,-1( هزاب یور f )ب .تسا هتسویپ (-∞,-1] هزاب یور f )فلا
ٔ ٔ
x
lim f (( =0 )ت .تسا هتسویپ [2,5] هزاب یور f )پ
x →5 ٔ
x
.تسا هتسویپ (-2,0( هزاب یور f )ج lim f (( =0 )ث
ٔ x →5 −
1٤1