Page 17 - C111211

یلیلحت ۀسدنه لوا سرد

ٔ
y ،دشاب AB طسو M رگا .دنتسه اهx روحم یور هاوخلد هطقن ود B و A ،لکش قباطم )پ
.دیروآ تسد هب ار M هطقن لوط
ٔ
A( x, ) M B( x, ) x
0
0
B
A
x A x B AB طسو M ⇒ AM = MB
⇒x M - x A = .......
y x + x
A
⇒2x M = ....... ⇒ x M = ..... B
y D D( ,y )0 D
،دشاب CD طسو N رگا .دنتسه اهy روحم یور هاوخلد هطقن ود D و C ،لباقم لکش رد )ت
ٔ
N
.دیبایب ار N هطقن ضرع
ٔ

....
y =
y C C( ,y )0 C CD طسو N ⇒ ................. ⇒ N
2
x

y
هجوت اب هاگنآ ،AB طسو هطقن M و دنشاب تاصتخم هحفص رد هاوخلد هطقن ود B و A رگا )ث
ٔ
ٔ
ٔ
A(x ,y )
y A A
A :داد ناشن ناوت یم لباقم لکش هب
....
y M = .... M(... , ... )
x + y + x y
. M ( A B , A B )زا تسا ترابع AB طخ هراپ طسو هطقن تاصتخم
ٔ
y B(x ,y ) 2 2
B B B

x
x A x M = .... x B
....

y
سلاک رد راک
11
10
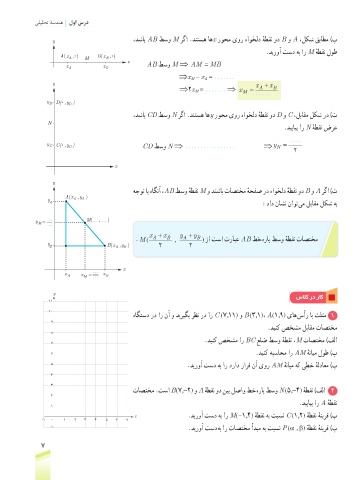
هاگتسد رد ار نآ و دیریگب رظن رد ار C (7,11) و B (3,1)، A(1,9) یاه سأر اب ثلثم 1
9
.دینک صخشم لباقم تاصتخم
8
.دینک صخشم ار BC علض طسو هطقن ،M تاصتخم )فلا
7 ٔ
ٔ
6 .دینک هبساحم ار AM هنایم لوط )ب
5 .دیروآ تسد هب ار دراد رارق نآ یور AM هنایم هک یطخ هلداعم )پ
ٔ
ٔ
4
3
تاصتخم .تسا B(7,-2) و A هطقن ود نیب لصاو طخ هراپ طسو N (5,-4) هطقن )فلا ٢
ٔ
ٔ
2
.دیبایب ار A هطقن
1 ٔ
x .دیروآ تسد هب ار M(-1,4) هطقن هب تبسن C (1,2) هطقن هنیرق )ب
ٔ
ٔ
ٔ
-1 0 1 2 3 4 5 6 7
.دیروآ تسد هب ار تاصتخم أدبم هب تبسن P (α , β) هطقن هنیرق )پ
-1
ٔ
ٔ
7