Page 71 - C112215

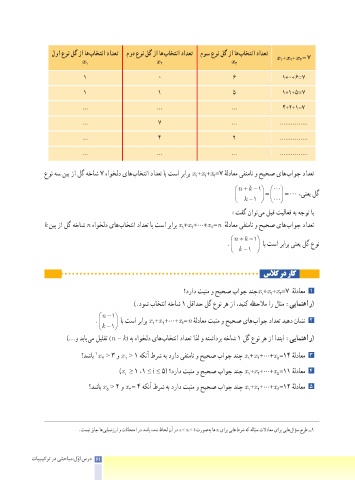
لوا عون لگ زا اه باختنا دادعت مود عون لگ زا اه باختنا دادعت موس عون لگ زا اه باختنا دادعت
x 1 + x 2 + x 3 = 7
x 1 x 2 x 3

1 0 6 1+0+6 = 7

1 1 5 1+1+5 = 7

… … … 4+2+1=7

… 7 … ……………

… 4 2 ……………

… … … ……………

عون هس نیب زا لگ هخاش 7 هاوخلد یاه باختنا دادعت اب تسا ربارب x +x +x =7 هلداعم یفنمان و حیحص یاه باوج دادعت
ٔ
3
2
1
+
 nk −  ⋅⋅⋅
1
=
   = ⋅⋅⋅ ،ینعی لگ
 k −1  ⋅⋅⋅ 
:تفگ ناوت یم لبق تیلاعف هب هجوت اب
…
k نیب زا لگ هخاش n هاوخلد یاه باختنا دادعت اب تسا ربارب x +x + +x k = n هلداعم یفنمان و حیحص یاه باوج دادعت
ٔ
2
1
 nk+−  1
.   اب تسا ربارب ینعی لگ عون
 k −1 
سلا ک رد را ک
سلاک رد راک
؟دراد تبثم و حیحص باوج دنچx +x +x =7 هلداعم 1
ٔ
2
3
1
).دوش باختنا هخاش 1 لقادح لگ عون ره زا ،دینک هظحلام ار لاثم :ییامنهار(
 n −  1
…
.   اب تسا ربارب x +x + +x k = n هلداعم تبثم و حیحص یاه باوج دادعت دیهد ناشن ٢
ٔ
1
2
 k −1 
)…و دبای یم لیلقت )n - k( هب هاوخلد یاه باختنا دادعت اذل و هتشادرب هخاش 1 لگ عون ره زا ادتبا :ییامنهار(
…
1
؟دشاب x > 3 و x > 1 هکنآ طرش هب دراد یفنمان و حیحص باوج دنچ x + x + +x =14 هلداعم ٣
ٔ
2
3
1
1
5
…
)x ≤ 1 ،1 ≥ i ≥ 5( ؟دراد تبثم و حیحص باوج دنچ x +x + +x =11 هلداعم ٤
ٔ
i
5
1
2
…
؟دشاب x > 2 و x = 4 هکنآ طرش هب دراد تبثم و حیحص باوج دنچ x +x + +x =12 هلداعم ٥
ٔ
1
2
5
3
6
.تسین زیاج اه یبایشزرا و تاناحتما رد دشاب هدش ظاحل نآ رد a ≤ x i ≤ b تروص هب اه x i یارب ییاه طرش هک هلایس تلاداعم یارب ییاه لاؤس حرط ــ1
ّ
تایبیکرت رد یثحابم:لّ وا سرد 61