Page 74 - C112213

→ →
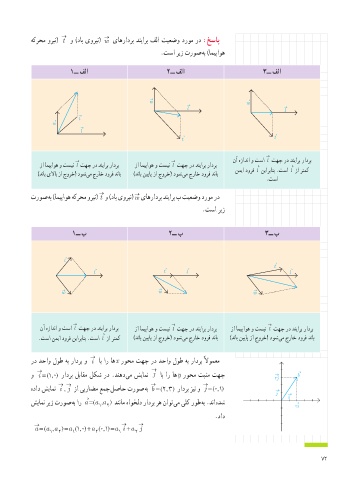
هکرحم ورین( t و )داب یورین( w یاهرادرب دنیارب فلا تیعضو دروم رد :خساپ

.تسا ریز تروص هب )امیپاوه

1ــ فلا 2ــ فلا 3ــ فلا

→
→ → نآ هزادنا و تسا l تهج رد دنیارب رادرب
زا امیپاوه و تسین l تهج رد دنیارب رادرب زا امیپاوه و تسین l تهج رد دنیارب رادرب → →
نمیا دورف l نیاربانب .تسا l زا رتمک
)دناب یلااب زا جورخ( دوش یم جراخ دورف دناب )دناب نییاپ زا جورخ( دوش یم جراخ دورف دناب
.تسا
→ →
تروص هب )امیپاوه هکرحم ورین( t و )داب یورین( w یاهرادرب دنیارب ب تیعضو دروم رد
.تسا ریز

1ــ ب 2ــ ب 3ــ ب

→ → →
نآ هزادنا و تسا l تهج رد دنیارب رادرب زا امیپاوه و تسین l تهج رد دنیارب رادرب زا امیپاوه و تسین l تهج رد دنیارب رادرب
→
.تسا نمیا دورف نیاربانب .تسا l زا رتمک )دناب نییاپ زا جورخ( دوش یم جراخ دورف دناب )دناب نییاپ زا جورخ( دوش یم جراخ دورف دناب

→
رد دحاو لوط هب رادرب و i اب ار اه x روحم تهج رد دحاو لوط هب رادرب لاومعم
ً
→ →
و i = ( ,) رادرب لباقم لکش رد .دنهد یم شیامن j اب ار اه y روحم تبثم تهج 3j b
10
→→ → →
هداد شیامن ,ij زا یبراضم عمج لصاح تروص هب b = (, ) رادرب زین و j = ( , )
01
23
j i
→
شیامن ریز تروص هب ار a = (, ) دننام هاوخلد رادرب ره ناوت یم یلک روط هب .دنا هدش 2i
aa
2
1
.داد
→ → →
a = ( ,a ) a ( , ) a ( , ) ai a j
=
=
+
+
10
a
1
0
1 2 1 2 1 2
72