Page 107 - C112214

99 قتشم : مراهچ لصف

نیرمت

.دنشابن ریذپ قتشم هطقن نیا رد یلو دنشاب هتسویپ x = 2 رد ود ره هک دینزب لاثم g و f دننام فلتخم عبات ود 1

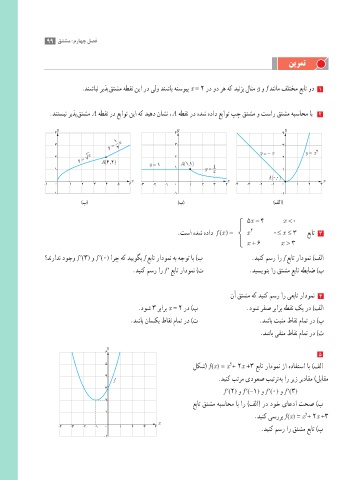
.دنتسین ریذپ قتشم A هطقن رد عباوت نیا هک دیهد ناشن ،A هطقن رد هدش هداد عباوت پچ قتشم و تسار قتشم هبساحم اب 2

y y y
4 4 4
1 x
3 y = 2 3 3
y = − x y = x 2
2 x 2 2
y = A (, ) y = A (, )
42
11
1 1 1 y = 1 1
x
A (, )
00
x x x
-1 0 1 2 3 4 5 6 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3
-1 -1 -1
)پ( )ب( )فلا(
5 x − x <4 0
.تسا هدش هداد () = x 2 0 ≤≤ 3 عبات 3
f
x
x
x + x >6 3
؟دنرادن دوجو f ′)3) و f ′)0) ارچ هک دییوگب f عبات رادومن هب هجوت اب )ب .دینک مسر ار f عبات رادومن )فلا
.دینک مسر ار f ′ عبات رادومن )ت .دیسیونب ار قتشم عبات هطباض )پ

نآ قتشم هک دینک مسر ار یعبات رادومن 4

.دوش 3 ربارب x = 2 رد )ب .دوش رفص ربارب هطقن کی رد )فلا
.دشاب ناسکی طاقن مامت رد )ت .دشاب تبثم طاقن مامت رد )پ

.دشاب یفنم طاقن مامت رد )ث

y
6
5
5 2
لکش( f )x) = x + 2x +3 عبات رادومن زا هدافتسا اب )فلا
4
f .دینک بترم یدوعص بیترت هب ار ریز ریداقم )لباقم
3
f ′)2) و f ′)-1) و f ′)0) و f ′)3)
2
عبات قتشم هبساحم اب ار )فلا( رد دوخ یاعدا تحص )ب
1
2
.دینک یسررب f )x) = x + 2x +3
x
-4 -3 -2 -1 0 1 2 3 4
.دینک مسر ار قتشم عبات )پ
-1