Page 11 - C112214

3 عبات : لوا لصف

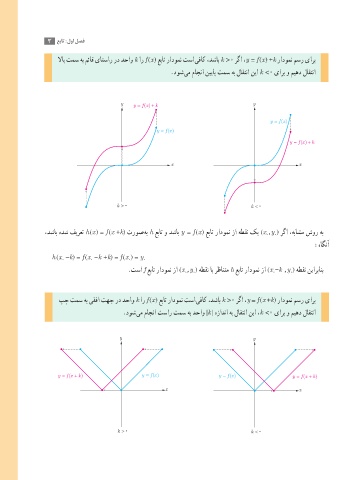
لااب تمس هب مئاق یاتسار رد دحاو k ار f (x) عبات رادومن تسا یفاک ،دشاب k >0 رگا ،y = f (x) +k رادومن مسر یارب

.دوش یم ماجنا نییاپ تمس هب لاقتنا نیا k <0 یارب و میهد لاقتنا

y y = fx + y
() k

y = fx
()
y = fx
()
y = fx +
() k

x x

k >0 k <0

،دشاب هدش فیرعت h (x) = f (x +k) تروص هب h عبات و دشاب y = f (x) عبات رادومن زا هطقن کی (x , y ) رگا ،هباشم شور هب
0

0

:هاگنآ
h (x -k) = f (x -k +k) = f (x ) = y 0
0
0
0
.تسا f عبات رادومن زا (x , y ) هطقن اب رظانتم h عبات رادومن زا (x -k , y ) هطقن نیاربانب
0
0
0
0
پچ تمس هب یقفا تهج رد دحاو k ار f (x) عبات رادومن تسا یفاک ،دشاب k >0 رگا ،y = f (x +k) رادومن مسر یارب

.دوش یم ماجنا تسار تمس هب دحاو |k | هزادنا هب لاقتنا نیا ،k <0 یارب و میهد لاقتنا

y y y y

y = fx y = ( fx + ) k y = ( fx + ) k y = fx y = fx y = ( fx + ) k y = ( fx + ) k y = fx
()
()
()
()
x x x x

k <0 k >0 k <0 k >0