Page 12 - C112214

4
π
=
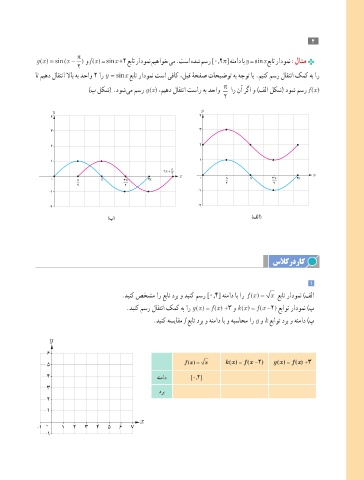
( ) sin( − ) و f (x) = sin x +2 عبات رادومن میهاوخ یم .تسا هدش مسر [0,2π] هنماد اب y = sin x عبات رادومن :لاثم
x
gx

2
ات میهد لاقتنا لااب هب دحاو 2 ار y = sin x عبات رادومن تسا یفاک ،لبق هحفص تاحیضوت هب هجوت اب .مینک مسر لاقتنا کمک هب ار
ٔ
π
)ب لکش( .دوش یم مسر g (x) ،میهد لاقتنا تسار هب دحاو ار نآ رگا و )فلا لکش( دوش مسر f (x)
2
y y
4 4

3 3

2 2

1 1
2 π+ π
2 x
0 π π 3 π 2π x 0 π π 3 π 2π
2 2 2 2
-1 -1

-2 -2
)ب( )فلا(

سلاکردراک

1
f
x
.دینک صخشم ار عبات درب و دینک مسر [0,4] هنماد اب ار () = x عبات رادومن )فلا
.دینک مسر لاقتنا کمک هب ار g (x) = f (x) +3 و k (x) = f (x -2) عباوت رادومن )ب

.دینک هسیاقم f عبات درب و هنماد اب و هبساحم ار g و k عباوت درب و هنماد )پ
y

6
(
(
(
(
()
5 fx = x k x ) = f x -2) g x ) = f x) +3
4 هنماد [0,4]
3
درب
2
1
x
-1 0 1 2 3 4 5 6 7
-1