Page 122 - C112214

114

ٔ
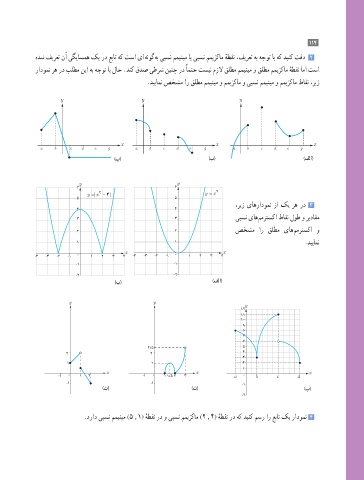
هدش فیرعت نآ یگیاسمه کی رد عبات هک تسا یا هنوگ هب یبسن ممینیم ای یبسن ممیزکام هطقن ،فیرعت هب هجوت اب هک دینک تقد 2
رادومن ره رد بلطم نیا هب هجوت اب لاح .دنک قدص یطرش نینچ رد ًامتح تسین مزلا قلطم ممینیم و قلطم ممیزکام هطقن اما تسا
ٔ
.دییامن صخشم ار قلطم ممینیم و ممیزکام و یبسن ممینیم و ممیزکام طاقن ،ریز

y y y

x x x
a b c d e g a b c d e g a b c d e g
)پ( )ب( )فلا(

y y y y y y
12 6 12 6 6 6
2
2
11 y = x 2 11 y = | x − 4 | y = x 2 y = | x − 4 |
10 5 10 5 5 5
9 9 ،ریز یاهرادومن زا کی ره رد 3
8 4 8 4 4 4
7 7 یبسن یاه ممرتسکا طاقن لوط و ریداقم
6 3 6 3 3 3
5 5
2
4 2 4 2 2 صخشم ار قلطم یاه ممرتسکا و
3 3
2 1 2 1 1 1 .دییامن
1 1
x x xx x x
a 0 b c d -4 -3 -2 -1 0 1 2 3 4 -4 a -3 0 -2 b -1 0 c 1 2 d 3 4 -4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4
-1 -1 -1 -1 -1 -1
-2 -2 -2 -2 -2 -2
)ب( )فلا(

y y y
12
11
10
9
8
7
6
2/5 5
2 2 4
3
1 1 2
1
x x x
-1 0 1 2 -1 0 1 1/5 2 3 a 0 b c d
-1 -1 -1
)ث( )ت( )پ(
-2

.دراد یبسن ممینیم (5 , 1) هطقن رد و یبسن ممیزکام (2 , 4) هطقن رد هک دینک مسر ار عبات کی رادومن 4
ٔ
ٔ